Cho hình hộp ABCD.A'B'C'D' có ABCD là hình thoi, \(AA' \bot \left( {ABCD} \right).\) Chứng minh rằng:
a) \(BB' \bot \left( {A'B'C'D'} \right);\)
b) \(BD \bot A'C.\)
Sử dụng định lý ba đường vuông góc.
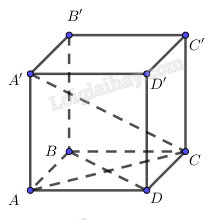
a) Vì ABCD.A'B'C'D' là hình hộp nên \(AA'{\rm{ // }}BB'.\) Mà \(AA' \bot \left( {ABCD} \right)\) nên \(BB' \bot \left( {ABCD} \right).\) Mặt khác \(\left( {ABCD} \right){\rm{ // }}\left( {A'B'C'D'} \right) \Rightarrow BB' \bot \left( {A'B'C'D'} \right).\)
b) Vì ABCD là hình thoi nên \(AC \bot BD.\) Do \(AA' \bot \left( {ABCD} \right)\) nên AC là hình chiếu của \(A'C\) trên mặt phẳng (ABCD). Theo định lí ba đường vuông góc suy ra \(BD \bot A'C.\)

Các bài tập cùng chuyên đề
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc. Vẽ đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) tại \(H\). Chứng minh \(AH \bot BC\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\sqrt 2 \), có các cạnh bên đều bằng \(2a\).
a) Tính góc giữa \(SC\) và \(AB\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(SAB\) trên mặt phẳng \(\left( {ABCD} \right)\).
Một cái lều có dạng hình lăng trụ \(ABC.A'B'C'\) có cạnh bên \(AA'\) vuông góc với đáy (Hình 24). Cho biết \(AB = AC = 2,4\) m; \(BC = 2\) m; \(AA' = 3\) m.
a) Tính góc giữa hai đường thẳng \(AA'\) và \(BC\); \(A'B'\) và \(AC\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\).
Cho hình lăng trụ ABC.A’B’C’ có H là trực tâm của tam giác ABC. Chứng minh rằng AH vuông góc với B’C’.
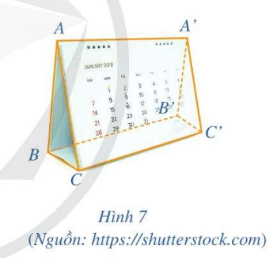
Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng \(AB \bot CC',\,\,\,AA' \bot BC\).
Bạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”. Bạn Hoa nói đúng hay sai? Vì sao?
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông.
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC).
b) Giả sử \(BC \bot SA, CA \bot SB\). Chứng minh rằng H là trực tâm của tam giác ABC và \(AB \bot SC\).
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
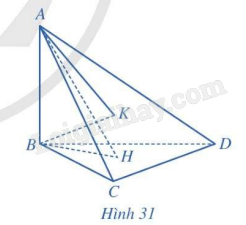
a) \(CD \bot (ABH)\).
b) \(CD \bot (ABK)\).
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm.
Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng:
a) SA \(\bot\) AD.
b) SC \(\bot\) CD.
Cho hình chóp S.ABCD có SA \(\bot\) (ABC), BC \(\bot\) AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Chứng minh rằng:
a) \(BC \bot \left( {OAH} \right)\).
b) H là trực tâm của \(\Delta ABC\).
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Cho hình lăng trụ ABC.A'B'C' có \(AA' \bot \left( {ABC} \right).\) Trong mặt phẳng (ABC), gọi H là hình chiếu của A trên BC. Chứng minh rằng \(BC \bot A'H.\)
Cho đoạn thẳng AB và mặt phẳng (P) sao cho \(\left( P \right) \bot AB\) và (P) cắt đoạn thẳng AB tại điểm H thoả mãn HA = 4 cm, HB = 9 cm. Điểm C chuyển động trong mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng điểm C thuộc đường tròn tâm H bán kính 6 cm trong mặt phẳng (P).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và \(SA \bot (ABCD)\). Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
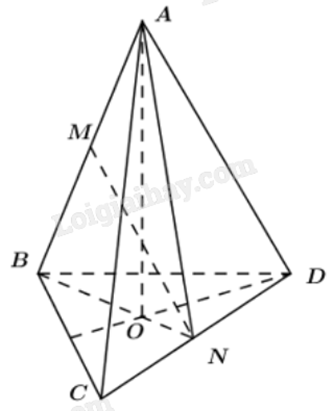
Tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây sai?
-
A.
\(AB \bot CD\)
-
B.
\(MN \bot AB\)
-
C.
\(MN \bot BD\)
-
D.
\(MN \bot CD\)







Danh sách bình luận