Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình bậc hai sau:
a) \({x^2} + 2x - 5 = 0\);
b) \(4{x^2} - 4\sqrt 3 x + 3 = 0\);
c) \({x^2} - 6\sqrt 5 x + 7 = 0\).
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b - \sqrt {\Delta '} }}{a}\).
+ Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b'}}{a}\).
+ Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.
a) Ta có: \(\Delta ' = {1^2} - 1.\left( { - 5} \right) = 6 > 0,\sqrt {\Delta '} = \sqrt 6 \) nên phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 1 - \sqrt 6 }}{1} = - 1 - \sqrt 6 ;{x_2} = \frac{{ - 1 + \sqrt 6 }}{1} = - 1 + \sqrt 6 \).
b) Ta có: \(\Delta ' = {\left( { - 2\sqrt 3 } \right)^2} - 4.3 = 0\) nên phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2}\).
c) Ta có: \(\Delta ' = {\left( { - 3\sqrt 5 } \right)^2} - 7.1 = 38 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = 3\sqrt 5 + \sqrt {38} ;{x_2} = 3\sqrt 5 - \sqrt {38} \).

Các bài tập cùng chuyên đề
Áp dụng công thức nghiệm, giải các phương trình sau:
a) \(2{x^2} - 5x + 1 = 0\);
b) \({x^2} + 8x + 16 = 0\);
c) \({x^2} - x + 1 = 0\).
Dùng công thức nghiệm của phương trình bậc hai, giải các phương trình sau:
a) \({x^2} - 2\sqrt 5 x + 2 = 0\);
b) \(4{x^2} + 28x + 49 = 0\);
c) \(3{x^2} - 3\sqrt 2 x + 1 = 0\).
Nhắc lại công thức tính hai nghiệm \({x_1},{x_2}\) của phương trình trên.
Các nghiệm của phương trình \({x^2} + 7x + 12 = 0\) là
A. \({x_1} = 3;{x_2} = 4\).
B. \({x_1} = - 3;{x_2} = - 4\).
C. \({x_1} = 3;{x_2} = - 4\).
D. \({x_1} = - 3;{x_2} = 4\).
Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức \(d = 0,05{v^2} + 1,1v\) để ước tính khoảng cách an toàn tối thiểu d (feet) (tức là độ dài quãng đường mà xe đi được kể từ khi đạp phanh đến khi xe dừng lại) đối với một phương tiện di chuyển với tốc độ v (dặm/ giờ) (theo Algebra 2, NXB MacGraw-Hill, 2008). Giả sử giới hạn tốc độ trên một đường cao tốc nào đó là 70 dặm/ giờ. Nếu một ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh thì ô tô đó có chạy nhanh hơn giới hạn tốc độ của đường cao tốc này không?
Cho phương trình bậc hai \({x^2} - 4x + 3 = 0\).
a) Thay mỗi dấu ? bằng số thích hợp để viết lại phương trình đã cho thành:
\({x^2} - 4x + 4 = ?\) hay \({\left( {x - 2} \right)^2} = ?\) (*)
b) Giải phương trình (*), từ đó tìm nghiệm của phương trình đã cho.
Giải các phương trình:
a) \(7{x^2} - 3x + 2 = 0\)
b) \(3{x^2} - 2\sqrt 3 x + 1 = 0\)
c) \( - 2{x^2} + 5x + 2 = 0\)
Trả lời câu hỏi trong Hoạt động khởi động (trang 11):
Sau khi được ném theo chiều từ dưới lên, độ cao h(m) của một quả bóng theo thời gian t (giây), được xác định bởi công thức h = 2 + 9t – 5t2 . Thời gian từ lúc ném cho đến khi bóng chạm đất là bao lâu?
Giải các phương trình:
a) x(x + 8) = 20
b) \(x(3x - 4) = 2{x^2} + 5\)
c) \({(x - 5)^2} + 7x = 65\)
d) \((2x + 3)(2x - 3) = 5(2x + 3)\)
Nghiệm của phương trình \({x^2} - 14x + 13 = 0\) là
A. \({x_1} = - 1;{x_2} = 13\)
B. \({x_1} = - 1;{x_2} = - 13\)
C. \({x_1} = 1;{x_2} = - 13\)
D. \({x_1} = 1;{x_2} = 13\)
Xét phương trình \(2{x^2} - 4x - 16 = 0\) (1)
Chia 2 vế của phương trình (1), ta được phương trình \({x^2} - 2x - 8 = 0\) (2)
a) Tìm số thích hợp cho “?” khi biến đổi phương trình (2) về dạng: ${{\left( x-? \right)}^{2}}=?$.
b) Từ đó, hãy giải phương trình 2.
c) Nêu các nghiệm của phương trình (1).
Giải các phương trình:
a) \(3{x^2} - x - 0,5 = 0\)
b) \(4{x^2} + 10x + 15 = 0\)
c) \( - {x^2} + x - \frac{1}{4} = 0\)
Biến đổi phương trình tổng quát ax2 + bx + c = 0 (a\( \ne \)0) theo các bước tương tự ví dụ 3, ta có:
\(\begin{array}{l}a{x^2} + bx + c = 0\\a{x^2} + bx = - c\\{x^2} + \frac{b}{a}x = \frac{{ - c}}{a}\\{x^2} + 2.x.\frac{b}{{2a}} + {\left( {\frac{b}{{2a}}} \right)^2} = \frac{{ - c}}{a} + {\left( {\frac{b}{{2a}}} \right)^2}\\{\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2} - 4ac}}{{4{a^2}}}.\end{array}\)
Đặt \(\Delta = {b^2} - 4ac\) và gọi là biệt thức của phương trình (\(\Delta \) là một chữ cái Hy Lạp, đọc là “đenta”). Ta được \({\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{\Delta }{{4{a^2}}}\). (1)
Giải phương trình (1) theo các hệ số a, b, c trong mỗi trường hợp sau:
a) \(\Delta \) > 0;
b) \(\Delta \) = 0
c) \(\Delta \) < 0.
Giải các phương trình sau:
a) \(3{x^2} - x + 2 = 0\)
b) \( - 3{t^2} + t + 6 = 0\)
c) \(3{x^2} - 6x + 3 = 0\)
Qua phân tích dữ liệu tại một cửa hàng tiện lợi, người ta thấy rằng nếu tăng giá bán của một loại nước ngọt thêm x (nghìn đồng) thì lợi nhuận P (nghìn đồng) thu về trong một tuần sau đó tính được theo công thức:
\(P = - 20{x^2} + 80x + 3300\)
Hỏi cửa hàng phải tăng giá của loại nước ngọt đó thêm bao nhiêu để lợi nhuận thu về trong tuần sau đó đạt mức 3380000 đồng?
Một bức tranh được treo bởi một khung tranh có chiều dài 80 cm, chiều rộng 60 cm và viền khung rộng x (cm) như Hình 6.6.
a) Viết biểu thức biểu thị diện tích của bức tranh.
b) Tìm x, biết diện tích bức tranh là 0,3996 m2.

Giải các phương trình sau:
a) \( - 2{x^2} + x + 1 = 0\)
b) \({x^2} - x + 4 = 0\)
c) \(4{x^2} - 4x + 1 = 0\)
d) \( - {x^2} - 4x + 1 = 0\)
e) \({y^2} - y - 3 = 0\)
g) \({z^2} - 2\sqrt 5 z + 5 = 0\)
Tìm các giá trị của m để phương trình \({x^2} - (m + 3)x + {m^2} = 0\) có nghiệm x = 1.
Giải các phương trình sau:
a) \({x^2} - x - 1 = 3x + 1\)
b) \(\frac{{{x^2} - 9}}{3} + 2 = x(1 - x)\)
c) \({\left( {x + 2} \right)^2} - 3(x + 2) + 2 = 0\)
d) \(2{x^4} + 3{x^2} - 2 = 0\)
Lượng nhiên liệu tiêu thụ y (l/100 km) của một số loại ô tô phụ thuộc vào tốc độ di chuyển x (km/h) theo hàm số \(y = \frac{1}{{320}}{x^2} - \frac{3}{8}x + \frac{{73}}{4}\) với \(20 \le x \le 140\). Hỏi ô tô đi với tốc độ nào thì lượng nhiên liệu tiêu thụ là 7 l/100 km?
Giải các phương trình sau:
a) \(2{x^2} - 3x - 2 = 0\)
b) \(3{y^2} + 4 = y\)
c) \({z^2} + 2\sqrt 3 z + 2 = 0\)
d) \( - {x^2} + 4\sqrt 3 z - 12 = 0\)
Phương trình nào sau đây vô nghiệm?
A. \(x(2x + 1) = \sqrt 5 \)
B. \(\frac{{{x^2} - 1}}{2} = 2(x - 3)\)
C. \(3{x^2} = x\left( {x - 5} \right)\)
D. \({x^2} - 2\sqrt 3 x + 3 = 0\)
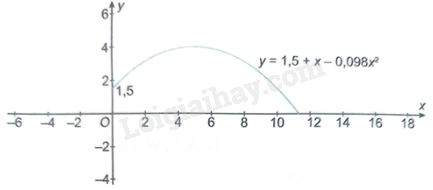
Quỹ đạo chuyển động của một quả bóng được cho bởi công thức \(y = 1,5 + x - 0,098{x^2}\), trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất.
Cho phương trình: \(\left( {m + 1} \right){x^2} - 3x + 1 = 0\).
a) Giải phương trình với \(m = 1\).
b) Tìm điều kiện của m để phương trình đã cho là phương trình bậc hai.
c) Tìm điều kiện của m để phương trình đã cho:
- Có hai nghiệm phân biệt;
- Có nghiệm kép;
- Vô nghiệm.
Độ cao h(t) (feet) của một vật sau t giây kể từ khi nó được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 85feet/giây được cho bởi công thức \(h\left( t \right) = - 16{t^2} + 85t\).
a) Khi nào thì vật ở độ cao 50 feet?
b) Vật có bao giờ đạt đến độ cao 120feet không? Giải thích lí do.
Trong một giải cờ vua thi đấu vòng tròn tính điểm, mỗi người chơi đấu với một người chơi khác đúng một lần. Công thức \(N = \frac{{{x^2} - x}}{2}\) dùng để tính số ván cờ N phải chơi theo thể thức thi đấu vòng tròn một lượt khi có x người chơi.
a) Nếu một giải đấu có 10 người chơi thì có tất cả bao nhiêu ván cờ?
b) Trong một giải cờ vua thi đấu vòng tròn có tất cả 36 ván cờ, hỏi có bao nhiêu người đã tham gia giải đấu?
Giải các phương trình:
a) 2x2 - 5x + 2 = 0
b) -x2 + 11x – 30 = 0
c) 5x2 -7x – 6 = 0
d) 5x2 - \(2\sqrt 5 \)x + 1 = 0
e) \(\frac{1}{{16}}{x^2} + \frac{1}{8}x = \frac{1}{2}\)
g) \({x^2} - \left( {\sqrt 5 - \sqrt 2 } \right)x - \sqrt {10} = 0\)
Giải các phương trình:
a) (x – 1)(2x + 3) = x2 + x
b) 4x(3x – 2) – 9x + 6 = 0
c) (x + 4)2 – (2x – 1)(2x + 1) = 14
d) (x + 3)(x + 4) – 4x = 20.
Cho phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có \(\Delta = {b^2} - 4ac = 0\). Khi đó, phương trình có hai nghiệm là
A. \({x_1} = {x_2} = - \frac{b}{{2a}}\)
B. \({x_1} = {x_2} = - \frac{b}{a}\)
C. \({x_1} = {x_2} = \frac{b}{{2a}}\)
D. \({x_1} = {x_2} = \frac{b}{a}\)
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho phương trình ax2 + bx + c = 0 \(\left( {a \ne 0} \right)\).
a) Khi \(\Delta = 0\), phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{b}{a}\).
b) Khi \(\Delta = 0\), phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{b}{{2a}}\).
c) Khi \(\Delta > 0\), phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}},{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}.\)
d) Khi b = 2b’; \(\Delta ' = b' - ac > 0\), phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt \Delta }}{a},{x_2} = \frac{{ - b' - \sqrt \Delta }}{a}.\)







Danh sách bình luận