Trong thực tiễn, có những tình huống đòi hỏi chúng ta phải xác định vị trí tương đối của hai đường thẳng, giao điểm của hai đường thẳng,... Chẳng hạn: Ở môn thể thao nội dung 10 m súng trường hơi di động, mục tiêu di động trên một đường thẳng b song song với mặt đất và cách mặt đất 1,4 m; viên đạn di động trên một đường thẳng a (Hình 39). Để bắn trúng mục tiêu, vận động viên phải ước lượng được giao điểm của và b sao cho thời gian chuyển động đến điểm của viên đạn và của mục tiêu là bằng nhau.
Làm thế nào để xác định giao điểm M của hai đường thẳng a và b?
Để xác định điểm M ta cần giải hệ phương trình gồm hai phương trình đường thẳng của hai đường thẳng a và b.
Các bài tập cùng chuyên đề
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) \({\rm{ }}{\Delta _1}:{\rm{ }}x + 4y - {\rm{3 }} = {\rm{ }}0,{\rm{ }}{\Delta _2}:{\rm{ }}x - 4y - 3{\rm{ }} = {\rm{ }}0\)
a) \({\rm{ }}{\Delta _1}:{\rm{ }}x + 2y - \sqrt 5 {\rm{ }} = {\rm{ }}0,{\rm{ }}{\Delta _2}:{\rm{ 2}}x + 4y - 3\sqrt 5 {\rm{ }} = {\rm{ }}0\)
Trong mặt phẳng tọa độ, cho hai đường thẳng
\(\begin{array}{l}{\Delta _1}:x - 2y + 3 = 0\\{\Delta _2}:3x - y - 1 = 0\end{array}\) .
a) Điểm \(M\left( {1;2} \right)\) có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\3x - y - 1 = 0\end{array} \right.\).
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của \({\Delta _1},{\Delta _2}\) với nghiệm của hệ phương trình trên.
Cho đường thẳng \(\Delta \): y= ax + b, với\(a \ne 0\) .
a) Chứng minh rằng \(\Delta \) cắt trục hoành.
b) Lập phương trình đường thẳng \({\Delta _o}\) đi qua O(0, 0) và song song (hoặc trùng) với\(\Delta \)
c) Hãy chỉ ra mối quan hệ giữa \({\alpha _\Delta }\) và \({\alpha _{{\Delta _o}}}\).
d) Gọi M là giao điểm của \({\Delta _o}\) với nửa đường tròn đơn vị và \({x_o}\) là hoành độ của M. Tính tung độ của M theo \({x_o}\) và a. Từ đó, chứng minh rằng \(\tan {\alpha _\Delta } = a\).
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) \({\Delta _1}:3\sqrt 2 x + \sqrt 2 y - \sqrt 3 = 0\) và \({\Delta _2}:6x + 2y - \sqrt 6 = 0\)
b) \({d_1}:x - \sqrt 3 y + 2 = 0\) và \({d_2}:\sqrt 3 x - 3y + 2 = 0\)
c) \({m_1}:x - 2y + 1 = 0\) và \({m_2}:3x + y - 2 = 0\)
Xét vị trí tương đối của các cặp đường thẳng \({d_1}\)và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:x - 5y + 9 = 0\) và \({d_2}:10x + 2y + 7 = 10\)
b) \({d_1}:3x - 4y + 9 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\end{array} \right.\)
c) \({d_1}:\left\{ \begin{array}{l}x = 5 + 4t\\y = 4 + 3t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 8t\\y = 1 + 6t\end{array} \right.\)
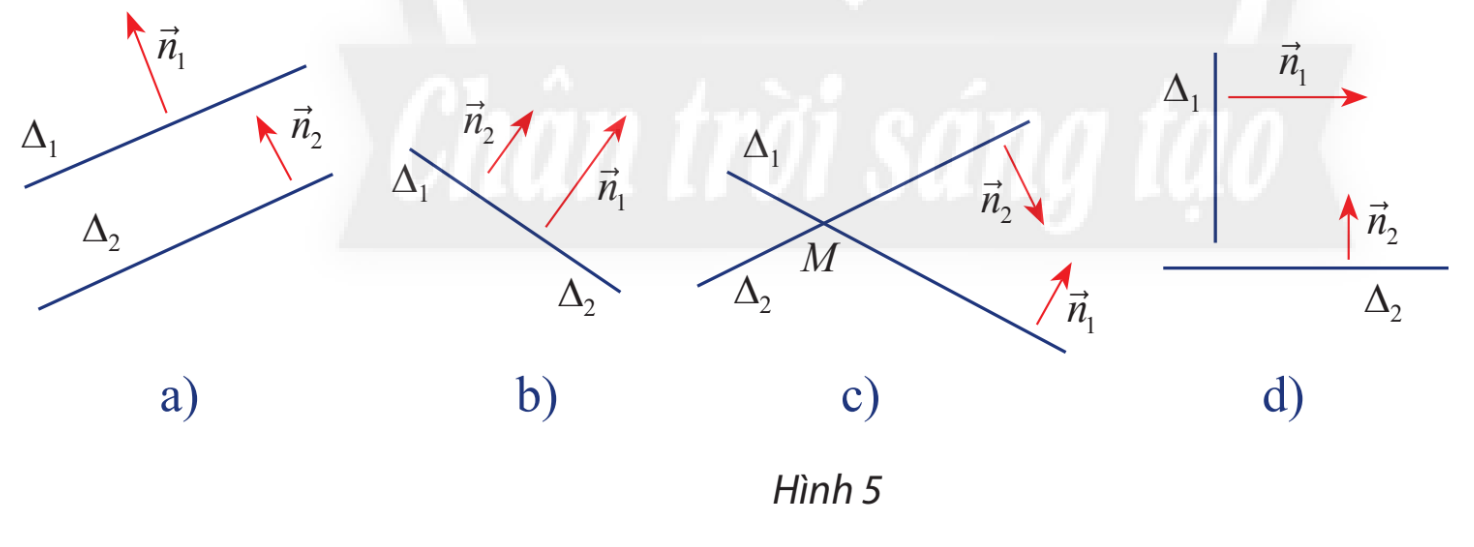
Cho hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) một vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Nêu nhận xét về vị trí tương đối giữa \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:
a) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương (hình 5a,b).
b) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương (hình 5c,d).
c) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc (hình 5d).
Xét vị trí tương đối của cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:
a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:5x - 2y + 9 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:3x + y - 11 = 0\)
Cho đường thẳng \(\Delta \) có phương trình tổng quát ax + bx + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng \(\Delta \) với các trục toạ độ trong môi trường hợp sau:
a) b = 0 và \(a \ne 0\)
b) \(b \ne 0\) và a = 0
c) \(b \ne 0\) và \(a \ne 0\)
Xét vị trí tương đối của đường thẳng d: x + 2y – 2 = 0 với mỗi đường thẳng sau:
\({\Delta _1}{\rm{: }}3x{\rm{ }}--{\rm{ }}2y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\); \({\Delta _2}:{\rm{ }}x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0\); \({\Delta _3}:{\rm{ }}2x{\rm{ }} + {\rm{ }}4y{\rm{ }}--{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Xét vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y = - 2 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2{t_2}\\y = - 3 + 2{t_2}\end{array} \right.\)
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Nêu điều kiện về hai vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) trong môi trường hợp sau:
a) \({\Delta _1}\) cắt \({\Delta _2}\)
b) \({\Delta _1}\) song song với \({\Delta _2}\)
c), \({\Delta _1}\) trùng với \({\Delta _2}\)
Nêu vị trí tương đối của hai đường thẳng trong mặt phẳng.
Xét vị trí tương đối của mỗi cặp đường thẳng sau
a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\);
b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\);
c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)
Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?
\({\Delta _1}:mx - y + 1 = 0\) và \({\Delta _2}:2x - y + 3 = 0\).
Xét vị trí tương đối của các cặp đường thẳng sau:
a) \(m:x + y - 2 = 0\) và \(k:2x + 2y - 4 = 0\).
b) \(a:\left\{ \begin{array}{l}x = 1 + 2t\\y = 4\end{array} \right.\) và \(b:\left\{ \begin{array}{l}x = 3t'\\y = 1 + t'\end{array} \right.\).
c) \({d_1}:x - 2y - 1 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 1 - 2t\\y = 2 - t\end{array} \right.\).
Cho đường thẳng \(d:4x + 3y - 2 = 0\) và đường thẳng \(k:\left\{ \begin{array}{l}x = - 1 + 3t\\y = 2 - 4t\end{array} \right.\). Vị trí tương đối của hai đường thẳng d và k là:
A. Trùng nhau
B. Song song
C. Cắt nhau nhưng không vuông góc
D. Vuông góc
Xét vị trí tương đối của các cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:
a) \({d_1}:2x + y + 9 = 0\) và \({d_2}:2x + 3y - 9 = 0\).
b) \({d_1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\end{array} \right.\) và \({d_2}:2x + y + 10 = 0\).
c) \({d_1}:\left\{ \begin{array}{l}x = 1 - t\\y = 8 - 5t\end{array} \right.\) và \({d_2}:5x - y + 3 = 0\).
Xét vị trí tương đối của mỗi cặp đường thẳng sau:
a) \({d_1}:2x - 3y + 5 = 0\) và \({d_2}:2x + y - 1 = 0\).
b) \({d_3}:\left\{ \begin{array}{l}x = - 1 - 3t\\y = 3 + t\end{array} \right.\) và \({d_4}:x + 3y - 5 = 0\).
c) \({d_5}:\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 + t\end{array} \right.\) và \({d_6}:\left\{ \begin{array}{l}x = - 2 + 2t'\\y = 1 - {t^'}\end{array} \right.\).
Cho hai đường thẳng ∆1: mx – 2y – 1 = 0 và ∆2: x - 2y + 3 = 0. Với giá trị nào của tham số m thì:
a) ∆1 // ∆2?
b) ∆1\( \bot {\Delta _2}\)?
