Xét vị trí tương đối của cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:

a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)

b) \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:5x - 2y + 9 = 0\)

c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:3x + y - 11 = 0\)

Xét vị trí tương đối giữa các cặp đường thẳng sau:

a) \({\rm{ }}{\Delta _1}:{\rm{ }}x + 4y - {\rm{3 }} = {\rm{ }}0,{\rm{ }}{\Delta _2}:{\rm{ }}x - 4y - 3{\rm{ }} = {\rm{ }}0\)

a) \({\rm{ }}{\Delta _1}:{\rm{ }}x + 2y - \sqrt 5 {\rm{ }} = {\rm{ }}0,{\rm{ }}{\Delta _2}:{\rm{ 2}}x + 4y - 3\sqrt 5 {\rm{ }} = {\rm{ }}0\)

Trong mặt phẳng tọa độ, cho hai đường thẳng

\(\begin{array}{l}{\Delta _1}:x - 2y + 3 = 0\\{\Delta _2}:3x - y - 1 = 0\end{array}\) .

a) Điểm \(M\left( {1;2} \right)\) có thuộc cả hai đường thẳng nói trên hay không?

b) Giải hệ \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\3x - y - 1 = 0\end{array} \right.\).

c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của \({\Delta _1},{\Delta _2}\) với nghiệm của hệ phương trình trên.

Cho đường thẳng \(\Delta \): y= ax + b, với\(a \ne 0\) .

a) Chứng minh rằng \(\Delta \) cắt trục hoành.

b) Lập phương trình đường thẳng \({\Delta _o}\) đi qua O(0, 0) và song song (hoặc trùng) với\(\Delta \)

c) Hãy chỉ ra mối quan hệ giữa \({\alpha _\Delta }\) và \({\alpha _{{\Delta _o}}}\).

d) Gọi M là giao điểm của \({\Delta _o}\) với nửa đường tròn đơn vị và \({x_o}\) là hoành độ của M. Tính tung độ của M theo \({x_o}\) và a. Từ đó, chứng minh rằng \(\tan {\alpha _\Delta } = a\).

Xét vị trí tương đối giữa các cặp đường thẳng sau:

a) \({\Delta _1}:3\sqrt 2 x + \sqrt 2 y - \sqrt 3  = 0\) và \({\Delta _2}:6x + 2y - \sqrt 6  = 0\)

b) \({d_1}:x - \sqrt 3 y + 2 = 0\) và \({d_2}:\sqrt 3 x - 3y + 2 = 0\)

c) \({m_1}:x - 2y + 1 = 0\) và \({m_2}:3x + y - 2 = 0\)

Xét vị trí tương đối của các cặp đường thẳng \({d_1}\)và \({d_2}\) trong các trường hợp sau:

a) \({d_1}:x - 5y + 9 = 0\) và \({d_2}:10x + 2y + 7 = 10\)

b)  \({d_1}:3x - 4y + 9 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\end{array} \right.\)

c) \({d_1}:\left\{ \begin{array}{l}x = 5 + 4t\\y = 4 + 3t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 8t\\y = 1 + 6t\end{array} \right.\)

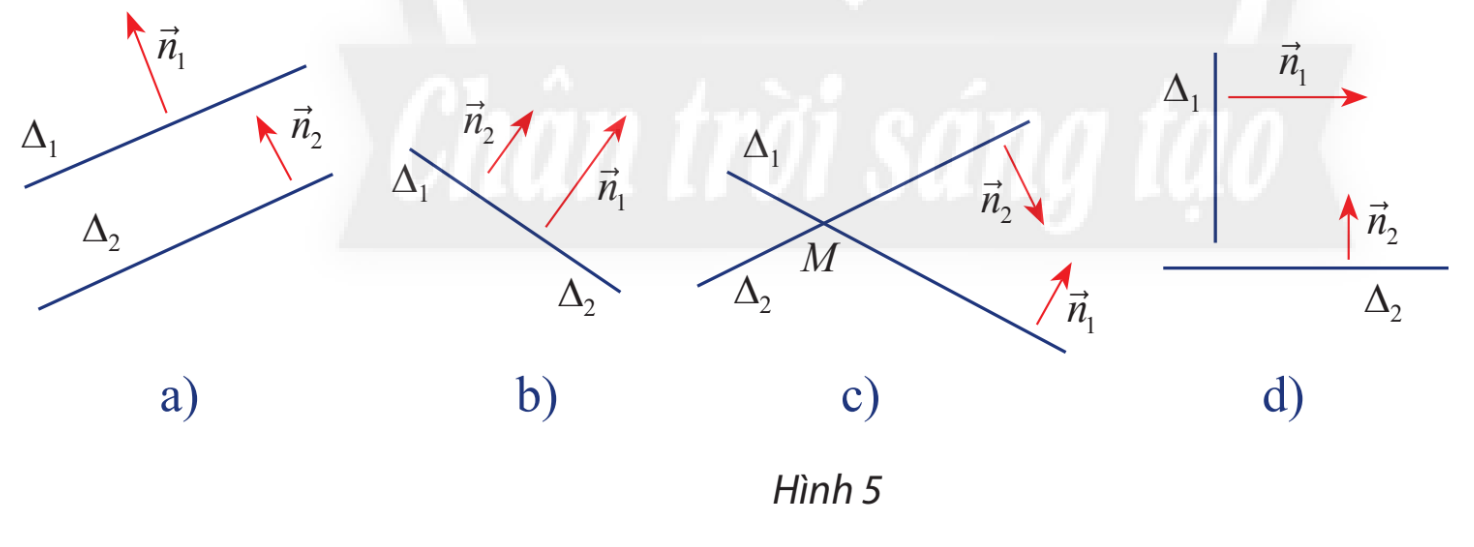
Cho hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) một vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).

Nêu nhận xét về vị trí tương đối giữa \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:

a) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương (hình 5a,b).

b) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương (hình 5c,d).

c) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc (hình 5d).

Cho đường thẳng \(\Delta \) có phương trình tổng quát ax + bx + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng \(\Delta \) với các trục toạ độ trong môi trường hợp sau:

a) b = 0 và \(a \ne 0\)

b) \(b \ne 0\) và a = 0

c) \(b \ne 0\) và \(a \ne 0\)

Xét vị trí tương đối của đường thẳng d: x + 2y – 2 = 0 với mỗi đường thẳng sau:

\({\Delta _1}{\rm{: }}3x{\rm{ }}--{\rm{ }}2y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\); \({\Delta _2}:{\rm{ }}x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0\); \({\Delta _3}:{\rm{ }}2x{\rm{ }} + {\rm{ }}4y{\rm{ }}--{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)

 Xét vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y =  - 2 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2{t_2}\\y =  - 3 + 2{t_2}\end{array} \right.\)

Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Nêu điều kiện về hai vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) trong môi trường hợp sau:

a) \({\Delta _1}\) cắt \({\Delta _2}\)

b) \({\Delta _1}\) song song với \({\Delta _2}\)

c), \({\Delta _1}\) trùng với \({\Delta _2}\)

Nêu vị trí tương đối của hai đường thẳng trong mặt phẳng.

Trong thực tiễn, có những tình huống đòi hỏi chúng ta phải xác định vị trí tương đối của hai đường thẳng, giao điểm của hai đường thẳng,... Chẳng hạn: Ở môn thể thao nội dung 10 m súng trường hơi di động, mục tiêu di động trên một đường thẳng b song song với mặt đất và cách mặt đất 1,4 m; viên đạn di động trên một đường thẳng a (Hình 39). Để bắn trúng mục tiêu, vận động viên phải ước lượng được giao điểm $M$ của $a$ và b sao cho thời gian chuyển động đến điểm $M$ của viên đạn và của mục tiêu là bằng nhau.

Làm thế nào để xác định giao điểm M của hai đường thẳng a và b?

Xét vị trí tương đối của mỗi cặp đường thẳng sau

a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\);

b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\);

c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x =  - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)

Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?

\({\Delta _1}:mx - y + 1 = 0\) và \({\Delta _2}:2x - y + 3 = 0\).

Xét vị trí tương đối của các cặp đường thẳng sau:

a) \(m:x + y - 2 = 0\) và \(k:2x + 2y - 4 = 0\).

b) \(a:\left\{ \begin{array}{l}x = 1 + 2t\\y = 4\end{array} \right.\) và \(b:\left\{ \begin{array}{l}x = 3t'\\y = 1 + t'\end{array} \right.\).

c) \({d_1}:x - 2y - 1 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 1 - 2t\\y = 2 - t\end{array} \right.\).

Cho đường thẳng \(d:4x + 3y - 2 = 0\) và đường thẳng \(k:\left\{ \begin{array}{l}x =  - 1 + 3t\\y = 2 - 4t\end{array} \right.\). Vị trí tương đối của hai đường thẳng d và k là:

A. Trùng nhau     

B. Song song       

C. Cắt nhau nhưng không vuông góc 

D. Vuông góc

Xét vị trí tương đối của các cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:

a) \({d_1}:2x + y + 9 = 0\) và \({d_2}:2x + 3y - 9 = 0\).

b) \({d_1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\end{array} \right.\) và \({d_2}:2x + y + 10 = 0\).

c) \({d_1}:\left\{ \begin{array}{l}x = 1 - t\\y = 8 - 5t\end{array} \right.\) và \({d_2}:5x - y + 3 = 0\).

Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a) \({d_1}:2x - 3y + 5 = 0\) và \({d_2}:2x + y - 1 = 0\).

b) \({d_3}:\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 3 + t\end{array} \right.\) và \({d_4}:x + 3y - 5 = 0\).

c) \({d_5}:\left\{ \begin{array}{l}x = 2 - 2t\\y =  - 1 + t\end{array} \right.\) và \({d_6}:\left\{ \begin{array}{l}x =  - 2 + 2t'\\y = 1 - {t^'}\end{array} \right.\).

Cho hai đường thẳng ∆₁: mx – 2y – 1 = 0 và ∆₂: x - 2y + 3 = 0. Với giá trị nào của tham số m thì:

a) ∆₁ // ∆₂?

b) ∆₁\( \bot {\Delta _2}\)?