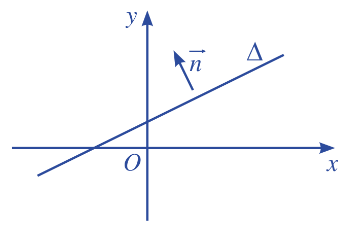
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \). Vẽ vectơ \(\overrightarrow n \) (\(\overrightarrow n \ne \overrightarrow 0 \)) có giá vuông góc với đường thẳng \(\Delta \).
Nhận xét
• Nếu \(\overrightarrow n \) là một vectơ pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \ne \overrightarrow 0 \left( {k \ne 0} \right)\) cũng là một vectơ pháp tuyến của \(\Delta \).
• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của đường thẳng đó.
• Nếu đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow u = \left( {a;b} \right)\) thì vectơ \(\overrightarrow n = \left( { - b;a} \right)\) là một vectơ pháp tuyến của \(\Delta \).
Các bài tập cùng chuyên đề
Hãy chỉ ra một vectơ pháp tuyển của đường thẳng \(\Delta :y = 3x + 4\).
Cho vectơ \(\overrightarrow n \ne \overrightarrow 0 \) và điểm A. Tìm tập hợp những điểm M sao cho \(\overrightarrow {AM} \) vuông góc với \(\overrightarrow n \).
Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\Delta :2x - 3y + 4 = 0\) ?
A. \(\overrightarrow {{n_1}} = \left( {3;2} \right)\)
B. \(\overrightarrow {{n_2}} = \left( {2;3} \right)\)
C. \(\overrightarrow {{n_3}} = \left( {3; - 2} \right)\)
D. \(\overrightarrow {{n_4}} = \left( {2; - 3} \right)\)
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :2x - y + 5 = 0\). Tìm tất cả vector pháp tuyến có độ dài \(2\sqrt 5 \) của đường thẳng \(\Delta \).
