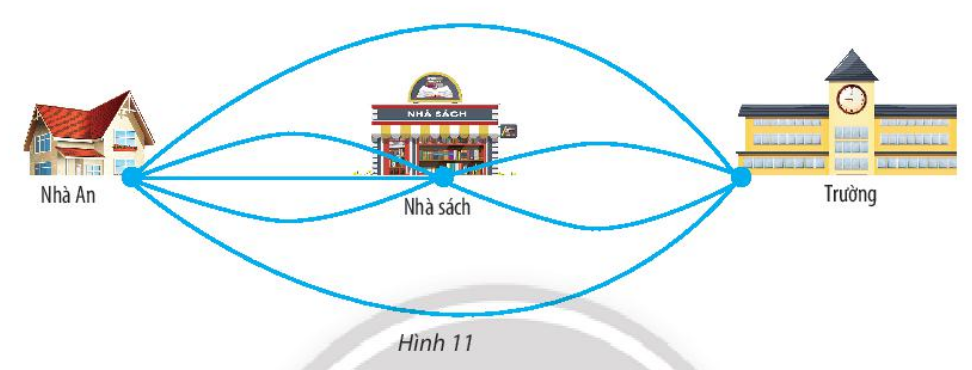
An có thể đi từ nhà đến trường theo các con đường như hình 11, trong đó có những con đường đi qua nhà sách.
a) An có bao nhiêu cách đi từ nhà đến trường mà có đi qua nhà sách?
b) An có bao nhiêu cách đi từ nhà đến trường?
Lưu ý: Chỉ tính những đường đi qua các điểm (nhà An, nhà sách, nhà trường) không quá 1 lần.
a) Bước 1: Xác định số cách đi từ nhà đến nhà sách, từ nhà sách đến trường
Bước 2: Áp dụng quy tắc nhân
b) Bước 1: Xác định số cách đi từ nhà đến trường qua nhà sách
Bước 2: Xác định số cách đi từ nhà đến trường không qua nhà sách
Bước 3: Áp dụng quy tắc cộng
a) Việc đi từ nhà đến trường qua nhà sách được thực hiện qua hai công đoạn:
Công đoạn 1: Đi từ nhà đến nhà sách, có 3 con đường.
Công đoạn 2: Đi từ nhà sách đến trường, có 2 con đường.
Số cách đi từ nhà đến trường qua nhà sách có số cách là:
\(3.2 = 6\)(cách)
b) Việc đi từ nhà đến trường có 2 phương án:
Phương án 1: Đi từ nhà đến trường qua nhà sách, có 6 cách thực hiện (kết quả của câu a)).
Phương án 2: Đi từ nhà đến trường không qua nhà sách có 2 cách.
Áp dụng quy tắc cộng, ta có số cách đi từ nhà đến trường là:
\(6 + 2 = 8\) (cách)

Các bài tập cùng chuyên đề
Một thùng chứa 6 quả dưa hấu, một thùng khác chứa 15 quả thanh long. Từ hai thùng này:
a) Có bao nhiêu cách chọn một quả dưa hấu hoặc một quả thanh long.
b) Có bao nhiêu cách chọn một quả dưa hấu và 1 quả thanh long.

Khối lớp 10 của một trường trung học phổ thông có ba lớp 10A, 10B, 10C. Lớp 10A có 30 bạn, lớp 10B có 35 bạn, lớp 10C có 32 bạn. Nhà trường muốn chọn 4 bạn để thành lập đội cờ đỏ của khối sao cho có đủ đại diện của các lớp. Hỏi có bao nhiêu cách lựa chọn?
Từ các chữ số 0, 1, 2, 3 có thể lập được bao nhiêu số thỏa mãn:
a) Là số tự nhiên có ba chữ số khác nhau?
b) Là số tự nhiên chẵn có ba chữ số khác nhau?
Có bao nhiêu số tự nhiên
a) Có 3 chữ số khác nhau
b) Là số lẻ có 3 chữ số khác nhau?
c) Là số có 3 chữ số và chia hết cho 5?
d) Là số có 3 chữ số khác nhau và chia hết cho 5?
Từ các chữ số 0; 1; 2; …. ;9, có thể lập được tất cả bao nhiêu số tự nhiên nhỏ hơn 1000, chia hết cho 5 và gồm các chữ số khác nhau?
Một trường trung học phổ thông được cử hai học sinh đi dự trại hè thành phố. Nhà trường quyết định chọn hai học sinh từ lớp 11A và lớp 12A. Biết rằng lớp 11A có 34 học sinh và lớp 12A có 36 học sinh. Hỏi nhà trường có bao nhiêu cách chọn nếu:
a) Hai học sinh được chọn khác lớp?
A. 70.
B. 1 224.
C. 34.
D. 36.
b) Hai học sinh được chọn cùng lớp?
A. 1 191.
B. 34.
C. 36.
D. 1 224.
Trong một cái hộp có chứa 8 quả bóng màu trắng đánh số từ 1 đến 8; 10 quả màu xanh đánh số từ 1 đến 10; 12 quả bóng màu cam đánh số từ 1 đến 12. Từ hộp này, có bao nhiêu cách?
a) Chọn ra một quả bóng?
b) Chọn ra ba quả bóng có màu khác nhau đôi một?
c) Chọn ra hai quả bóng có màu khác nhau?
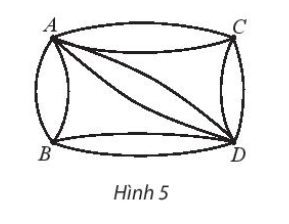
Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5. Có bao nhiêu cách chọn đường đi khác nhau:
a) Từ A qua B rồi đến D.
b) Từ A đến D.
Lưu ý: Mỗi đường đi qua mỗi ngôi làng ít nhất 1 lần.
Tung đồng thời hai con xúc xắc khác nhau và ghi lại số chấm xuất hiện trên mỗi con xúc xắc. Có bao nhiêu kết quả có thể xảy ra mà tổng số chấm xuất hiện trên hai mặt là bội của 5?
Sử dụng 5 chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên:
a) Có ba chữ số khác nhau?
b) Có 3 chữ số khác nhau và bé hơn 300?
c) Có các chữ số khác nhau và bé hơn 100?
Một nhóm có 4 học sinh, mỗi học sinh chọn một trong ba lớp môn thể thao: bóng đá, bóng rổ và cầu lông. Có bao nhiêu kết quả khác nhau về sự chọn của các học sinh trong nhóm?
A. \({3^4}\)
B. \({4^3}\)
C. \(3!\)
D. \(4!\)
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số có ba chữ số khác nhau chứa chữ số 2 và chia hết cho 5?
-
A.
20
-
B.
21
-
C.
22
-
D.
23







Danh sách bình luận