Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
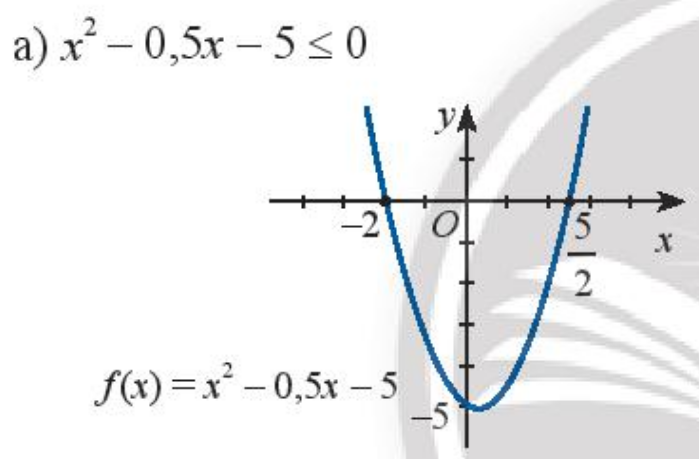
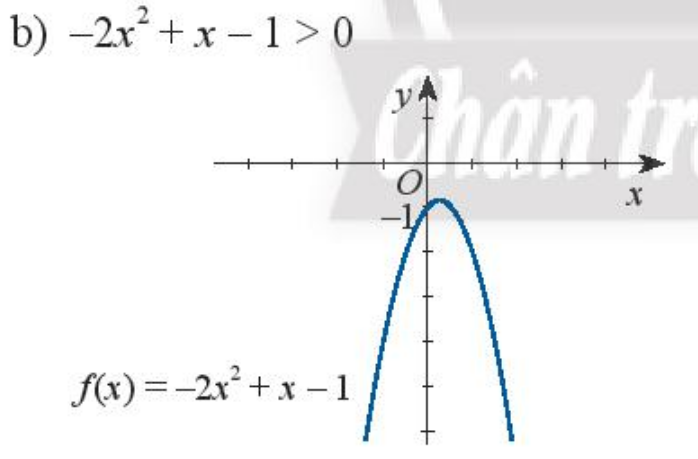
Quan sát vào đồ thị ta thấy
+) Tại giao điểm của đồ thị và trục hoành là nghiệm của \(f\left( x \right) = 0\)
+) Khoảng của x mà phần độ thị nằm trên trục hoành là nghiệm của \(f\left( x \right) > 0\)
+) Khoảng của x mà phần độ thị nằm dưới trục hoành là nghiệm của \(f\left( x \right) < 0\)
a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { - 2;\frac{5}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} - 0,5x - 5 \le 0\) là đoạn \(\left[ { - 2;\frac{5}{2}} \right]\)
b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành
Vậy nghiệm của bất phương trình \( - 2{x^2} + x - 1 > 0\) vô nghiệm

Các bài tập cùng chuyên đề
Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).
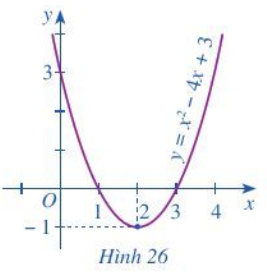
Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 5x + 3 > 0\)
b) \( - {x^2} - 2x + 8 \le 0\)
c) \(4{x^2} - 12x + 9 < 0\)
d) \( - 3{x^2} + 7x - 4 \ge 0\)
Tìm m để phương trình \(2{x^2} + \left( {m + 1} \right)x + m - 8 = 0\) có nghiệm.
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là:
-
A.
(1; 2)
-
B.
\(\left( {-\infty ;{\rm{ }}1} \right){\rm{ }} \cup {\rm{ }}\left( {2;{\rm{ }} + \infty } \right)\)
-
C.
\(\left( {-\infty ;{\rm{ }}1} \right)\)
-
D.
\(\left( {2;{\rm{ }} + \infty } \right)\)
Tập nghiệm của bất phương trình \({x^2}-{\rm{ }}1{\rm{ }} > {\rm{ }}0\) là:
-
A.
\(\left( {1; + \infty } \right)\)
-
B.
\(\left( { - 1; + \infty } \right)\)
-
C.
(– 1; 1);
-
D.
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
Tập nghiệm của bất phương trình \( - {x^2} + 3x + 18 \ge 0\) là:
A. \(\left[ { - 3;6} \right]\)
B. \(\left( { - 3;6} \right)\)
C. \(x \in \left( { - \infty ; - 3} \right) \cup \left( {6; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 3} \right] \cup \left[ {6; + \infty } \right)\)
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 8x + 5 > 0\)
b) \( - 2{x^2} - x + 3 \le 0\)
c) \(25{x^2} - 10x + 1 < 0\)
d) \( - 4{x^2} + 5x + 9 \ge 0\)
Tìm giao các tập nghiệm của hai bất phương trình \( - 3{x^2} + 7x + 10 \ge 0\) và \( - 2{x^2} - 9x + 11 > 0\).
Tìm \(m\) để phương trình \( - {x^2} + \left( {m + 2} \right)x + 2m - 10 = 0\) có nghiệm.
Tập nghiệm của bất phương trình \( - 5{x^2} + 6x + 11 \le 0\) là:
A. \(\left[ { - 1;\frac{{11}}{5}} \right]\)
B. \(\left( { - 1;\frac{{11}}{5}} \right)\)
C. \(x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\)
Giải các bất phương trình bậc hai sau:
a) \(4{x^2} - 9x + 5 \le 0\)
b) \( - 3{x^2} - x + 4 > 0\)
c) \(36{x^2} - 12x + 1 > 0\)
d) \( - 7{x^2} + 5x + 2 < 0\)
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Giải các bất phương trình bậc hai:
a) \({x^2} - 1 \ge 0\)
b) \({x^2} - 2x - 1 < 0\)
c) \( - 3{x^2} + 12x + 1 \le 0\)
d) \(5{x^2} + x + 1 \ge 0\)
Bất phương trình \({x^2} - 2mx + 4 > 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\) khi
A. \(m = - 1.\)
B. \(m = - 2.\)
C. \(m = 2.\)
D. \(m > 2.\)
Giải các bất phương trình sau:
a) \(2{x^2} - 3x + 1 > 0\)
b) \({x^2} + 5x + 4 < 0\)
c) \( - 3{x^2} + 12x - 12 \ge 0\)
d) \(2{x^2} + 2x + 1 < 0.\)
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
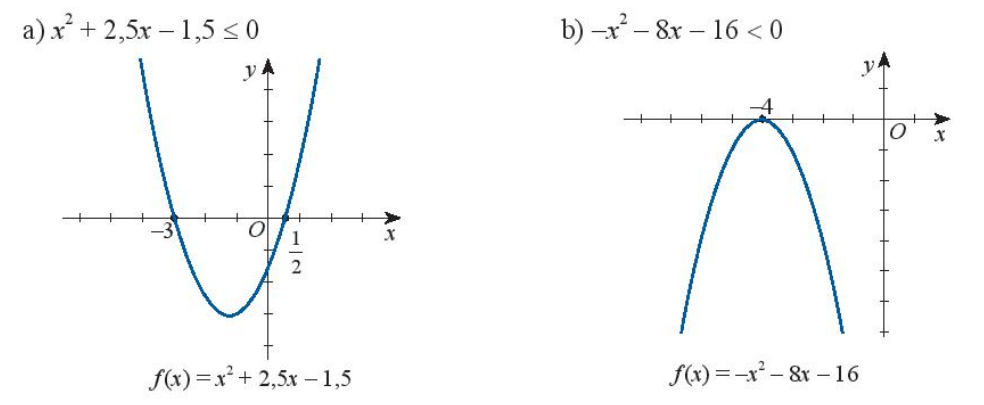
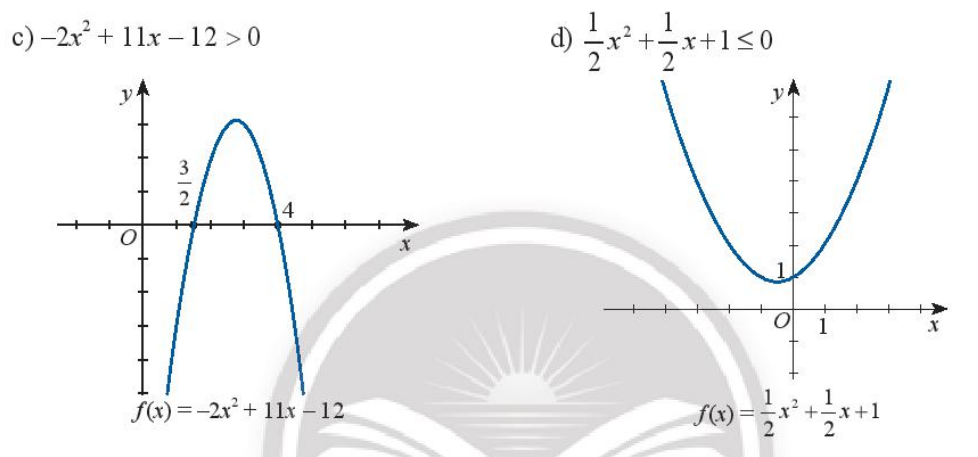
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 15x + 28 \ge 0\)
b) \( - 2{x^2} + 19x + 255 > 0\)
c) \(12{x^2} < 12x - 8\)
d) \({x^2} + x - 1 \ge 5{x^2} - 3x\)
Giải các bất phương trình sau:
a) \(7{x^2} - 19x - 6 \ge 0\)
b) \( - 6{x^2} + 11x > 10\)
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1\)
d) \({x^2} - 10x + 25 \le 0\)
Số giá trị nguyên của tham số \(m\) trên đoạn \(\left[ { - 10;10} \right]\) để bất phương trình \(m{x^2} - 2mx + 2m - 1 \le 0\) thỏa mãn với mọi \(x \in \mathbb{R}\) là:
-
A.
10
-
B.
11
-
C.
18
-
D.
20
Giải các bất phương trình sau:
a) \(3{x^2} - 36x + 108 > 0\)
b) \( - {x^2} + 2x - 2 \ge 0\)
c) \({x^4} - 3{x^2} + 2 \le 0\)
d) \(\frac{1}{{{x^2} - x + 1}} \le \frac{1}{{2{x^2} + x + 2}}\)
Tìm các giá trị của tham số m để phương trình \({x^2} - 2(m - 1)x + 4{m^2} - m = 0\) (1)
a) Có hai nghiệm phân biệt.
b) Có hai nghiệm trái dấu.
Tìm các giá trị của tham số m để:
a) \( - {x^2} + (m + 1)x - 2m + 1 \le 0,\forall x \in \mathbb{R}\)
b) \({x^2} - (2m + 1)x + m + 2 > 0,\forall x \in \mathbb{R}\)
Tập nghiệm của bất phương trình \({x^2} - 4x + 3 < 0\) là:
A. \((1;3)\)
B. \(( - \infty ;1) \cup {\rm{[}}3; + \infty )\)
C. \({\rm{[}}1;3]\)
D. \(( - \infty ;1] \cup {\rm{[}}4; + \infty )\)
Các giá trị của tham số m làm cho biểu thức \(f(x) = {x^2} + 4x + m - 5\) luôn dương là:
A. m ≥ 9
B. m > 9
C. Không có m
D. m < 9







Danh sách bình luận