Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh:
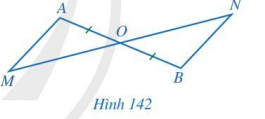
a) Nếu OM = ON thì AM // BN;
b) Nếu AM // BN thì OM = ON.
Chứng minh dựa vào chứng minh hai tam giác AOM và BON bằng nhau.
a) Xét tam giác AOM và tam giác BON có:
OA = OB;
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
OM = ON.
Vậy \(\Delta AOM = \Delta BON\)(c.g.c).
Suy ra: \(\widehat {AMO} = \widehat {BNO}\) (2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AM // BN.
b) Ta có: AM // BN nên \(\widehat {MAO} = \widehat {NBO}\)(hai góc so le trong).
Xét tam giác AOM và tam giác BON có:
\(\widehat {MAO} = \widehat {NBO}\)
OA = OB;
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
Vậy \(\Delta AOM = \Delta BON\)(g.c.g). Suy ra: OM = ON ( 2 cạnh tương ứng).

Các bài tập cùng chuyên đề
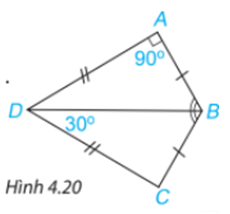
Cho Hình 4.20, biết \(AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }\)
a) Chứng minh rằng \(\Delta ABD = \Delta CBD\).
b) Tính \(\widehat {ABC}\).
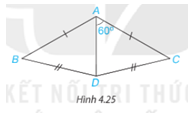
Cho Hình 4.25, biết \(\widehat {DAC} = {60^\circ },AB = AC,DB = DC\). Hãy tính \(\widehat {DAB}\).
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).
b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh OE là tia phân giác của góc xOy
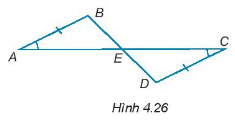
Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng AB = CD, \(\widehat {BAE} = \widehat {DCE}\). Chứng minh rằng:
a) E là trung điểm của các đoạn thẳng AC và BD.
b) \(\Delta ACD = \Delta CAB\)
c) AD song song với BC.
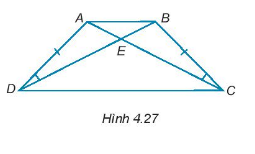
Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC, \(\widehat {ADE} = \widehat {BCE}\). Chứng minh rằng:
a) \(\widehat {DAC} = \widehat {CBD}\)
b) \(\Delta AED = \Delta BEC.\)
c) \(AB//DC\)
Cho tam giác ABC bằng tam giác DEF (h.4.28)
a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng
AM = DN.
b) Trên hai cạnh AC và DF lấy 2 điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc ABC và DEF. Chứng minh rằng
BP = EQ.

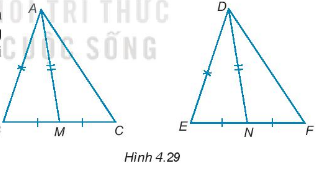
Gọi M, N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng \(\Delta ABC = \Delta DEF\)
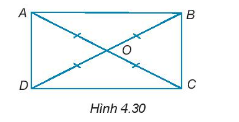
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như H4.30. Chứng minh ABCD là hình chữ nhật.
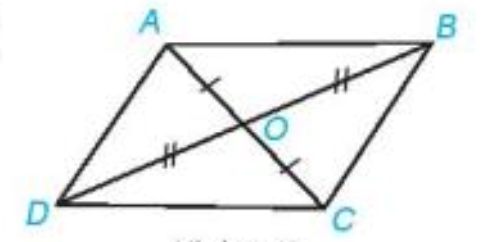
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình vẽ.
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.
b) Chứng minh rằng \(\Delta DAB = \Delta BCD\).
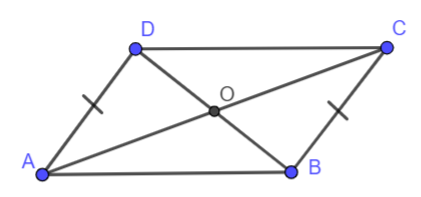
Cho hình vẽ dưới đây. Biết đường thẳng AD song song với đường thẳng BC, AD = BC. Chứng minh rằng AB song song với CD.
Cho năm điểm A, B,C,D,O như hình vẽ. Biết rằng OA = OB, OC = OD.
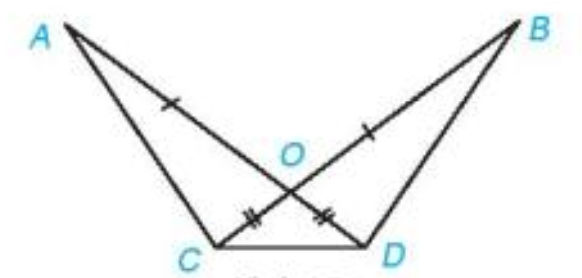
a) Chứng minh rằng AC=BD.
b) Chứng minh rằng \(\Delta ACD = \Delta BDC\)
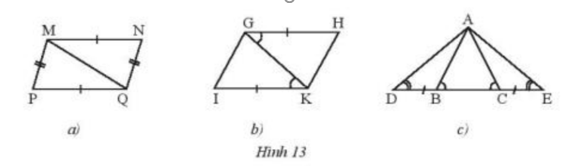
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
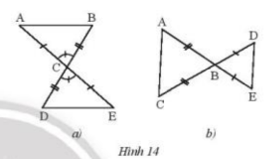
Hai tam giác trong mỗi hình bên (Hình 14a,b) có bằng nhau không? Vì sao?
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.
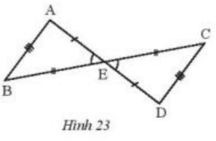
a) \( \Delta ABE = ?\)
b) \( \Delta EAB = ?\)
c) \( ? = \Delta CDE\)
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) \(\Delta EAB=\Delta ECD\)
c) OE là tia phân giác của góc xOy.
Cho góc bẹt \(xOy\) có tia phân giác \(Ot\). Trên tia \(Ot\) lấy hai điểm \(A, B\) (\(A\) nằm giữa \(O\) và \(B\)). Lấy điểm \(C \in Ox\) sao cho \(OC = OB\), lấy điểm \(D \in Oy\) sao cho \(OD = OA\). Gọi \(M, N\) lần lượt là trung điểm của \(AC\) và \(BD\).
Tính các góc của tam giác \(MON\).
Cho \(\Delta ABC\) cân tại A và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho \(NK = NC\). Chứng minh rằng:
a) \(\Delta ABM = \Delta ACM\).
b) \(AM \bot BC\).
c) \(AK = 2.MB\).
d) \(KA \bot AM\).
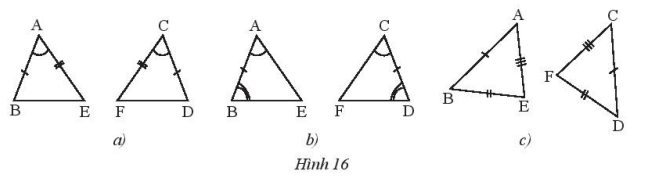
Các cặp tam giác trong Hình 16 có bằng nhau không? Nếu có, chúng bằng nhau theo trường hợp nào?
Cho tam giác ABC có \(\hat A = 90^\circ \), M là trung điểm của BC. Chứng minh BC = 2AM.
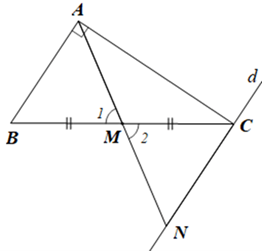
Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a)\(\Delta MBC = \Delta MDC,\Delta MAC = \Delta MEC\)
b)\(\Delta MAB = \Delta MED\)
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho \(DM = DC\).
a) Chứng minh rằng \(\Delta ADM = \Delta BDC\). Từ đó suy ra \(AM = BC\) và AM//BC.
b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho \(EN = EB\). Chứng minh rằng AN//BC.
c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của \(\widehat {BAC}\) cắt nhau tại K. Chứng minh rằng \(\Delta BKM = \Delta CKN\) từ đó suy ra KC vuông góc với AN.
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của \(\widehat {BAC}\) cắt nhau tại K. Chứng minh rằng \(\Delta BKM = \Delta CKN\) từ đó suy ra KC vuông góc với AN.







Danh sách bình luận