Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình 6). Làm thế nào để các định được bán kính của đĩa cổ này?
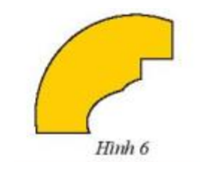
Sử dụng tính chất của điểm giao 2 trung trực trong tam giác
Gọi O là tâm của chiếc đĩa
\( \Rightarrow \) OA = OB = OC = r ( do cùng có độ dài = bán kính )
Xét tam giác ABC có O là điểm cách đều A, B, C
\( \Rightarrow \) O là giao của 3 đường trung trực tam giác ABC
Để xác định O ta vẽ 2 đường trung trực của AB, BC chúng cắt nhau tại O .

Các bài tập cùng chuyên đề
Điểm cách đều ba đỉnh của tam giác là:
-
A.
Giao điểm của ba đường cao
-
B.
Giao điểm của ba đường trung tuyến
-
C.
Giao điểm của ba đường phân giác
-
D.
Giao điểm của ba đường trung trực
Vẽ tam giác ABC ( không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38)
a) Tại sao OB = OC, OC = OA.
b) Điểm O có nằm trên đường trung trực của AB không?
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
Em hãy trả lời câu hỏi trong tình huống mở đầu.
Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều 3 đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
a) Có một chi tiết máy ( đường viền ngoài là đường tròn) bị gãy. (H.9.46). Làm thế nào để xác định được bán kính của đường viền này ?
b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ một điểm M cách đều A, B, C để quy hoạch một trường học

Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?
Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.
Vẽ ba đường trung trực của tam giác ABC vuông tại A.
Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC của tam giác ABC (Hình 2).
- Hãy so sánh độ dài của ba đoạn thẳng OA, OB, OC
- Theo em đường trung trực ứng với cạnh BC có đi qua điểm O hay không?
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
Trên bản đồ quy hoạch một khu dân cư có ba điểm A, B, C (Hình 5). Tìm địa điểm M để xây một trường học sao cho trường học này cách đều ba điểm dân cư đó.
Vẽ ba tam giác nhọn, vuông, tù
a) Xác định điểm O cách đều ba đỉnh của mỗi tam giác
b) Nêu nhận xét của em về vị trí của điểm O trong mỗi trường hợp.
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC, PO vuông góc với AC.
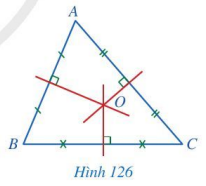
Quan sát các đường trung trực của tam giác ABC (Hình 126), cho biết ba đường trung trực đó có cùng đi qua một điểm hay không
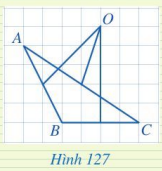
Trong Hình 127, điểm O có phải là giao điểm của ba đường trung trực của tam giác ABC không?
Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm của ba đường trung trực của tam giác ABC.
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS.
Điểm O trong hình 7 có phải là giao điểm của ba đường trung trực của tam giác ABC hay không? Hãy giải thích.

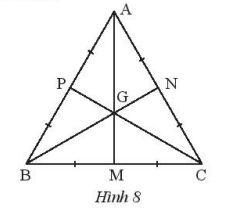
Cho tam giác đều ABC và điểm G như trong hình 8. Hãy chứng minh GA = GB = GC.
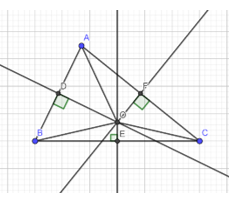
Cho tam giác ABC có góc A là góc từ. Các đường trung trực của AB và Ac cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh
a) \(\Delta EO{\rm{A}} = \Delta EOB,\Delta F{\rm{O}}A = \Delta F{\rm{O}}C\)
b) Chứng minh rằng AO là tia phân giác của góc EAF.
Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Đường thẳng BC là đường trung trực của AD.
b) Điểm I cách đều các điểm A, B, D.
c) Điểm B nằm trên đường trung trực của CD.
d) Điểm C không nằm trên đường trung trực của BD.
Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo các góc của tam giác ABC.
Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.







Danh sách bình luận