Inch ( đọc là in-sơ và viết tắt là in) là tên của một đơn vị chiều dài trong Hệ đo lường Mĩ. Biết rằng 1 in = 2,54 cm.
a) Hỏi một người cao 170 cm sẽ có chiều cao là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?
b) Chiều cao của một người tính theo xentimet có tỉ lệ thuận với chiều cao của người đó tính theo inch không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
Chiều dài (theo cm) = 2,54. Chiều dài (theo inch)
a) Chiều cao của người đó là:
\(170 : 2,54 \approx 66,9 \approx 67 \)( inch)
b) Chiều cao của một người tính theo xentimet có tỉ lệ thuận với chiều cao của người đó tính theo inch vì chúng liên hệ với nhau theo công thức: Chiều dài (theo cm) = 2,54. Chiều dài (theo inch)
Hệ số tỉ lệ là 2,54.

Các bài tập cùng chuyên đề
Một chiếc máy bay bay với vận tốc không đổi là 900 km/h.
Quãng đường s (km) mà máy bay đó bay được và thời gian di chuyển t (h) là hai đại lượng liên hệ với nhau như thế nào?
Chiều dài x (m) và khối lượng m (kg) của thanh sắt phi 18 được liên hệ theo công thức m= 2x. Tìm số thích hợp cho ? trong bảng sau:
|
x (m) |
2 |
3 |
5 |
8 |
|
m (kg) |
? |
? |
? |
? |
Một ô tô chuyển động đều với vận tốc 65 km/h.
a) Viết công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động.
b) s và t có phải là hai đại lượng tỉ lệ thuận không? Nếu có hãy xác định hệ số tỉ lệ của s đối với t.
c) Tính giá trị của s khi t = 0,5; t = \(\frac{3}{2}\); t = 2.
Cho biết x, y là hai đại lượng tỉ lệ thuận với nhau:
|
x |
x1 = 3 |
x2 = 5 |
X3 = 7 |
|
y |
y1 = 9 |
y2 = 15 |
y3 = 21 |
a) Hãy xác định hệ số tỉ lệ của y đối với x
b) So sánh các tỉ số: \(\frac{{{y_1}}}{{{x_1}}},\frac{{{y_2}}}{{{x_2}}},\frac{{{y_3}}}{{{x_3}}}\)
c) So sánh các tỉ số: \(\frac{{{x_1}}}{{{x_2}}}\) và \(\frac{{{y_1}}}{{{y_2}}}\); \(\frac{{{x_1}}}{{{x_3}}}\) và \(\frac{{{y_1}}}{{{y_3}}}\)
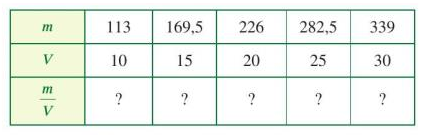
Các giá trị tương ứng của khối lượng m (g) và thể tích V (cm3) được cho bởi bảng sau:
a) Tìm số thích hợp cho
b) Hai đại lượng m và V có tỉ lệ thuận với nhau không? Vì sao?
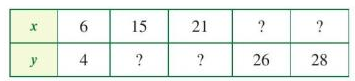
Cho biết x, y là hai đại lượng tỉ lệ thuận với nhau:
a) Xác định hệ số tỉ lệ của y đối với x. Viết công thức tính y theo x.
b) Xác định hệ số tỉ lệ của x đối với y. Viết công thức tính x theo y.
c) Tìm số thích hợp cho
Đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ \(\frac{1}{3}\) khi:
-
A.
xy = 3;
-
B.
\(xy = \frac{1}{3};\)
-
C.
x = 3y;
-
D.
y = 3x.
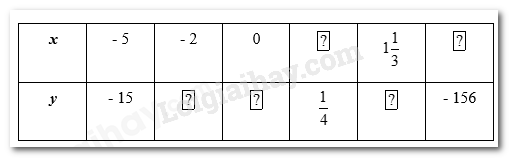
Cho biết x, y là hai đại lượng tỉ lệ thuận với nhau. Tìm số thích hợp cho ?:
Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ là – 2; z tỉ lệ thuận với y theo hệ số tỉ lệ là – 3; t tỉ lệ thuận với z theo hệ số tỉ lệ là 4. Chứng tỏ rằng t tỉ lệ thuận với x và tìm hệ số tỉ lệ đó.
Cho biết x, y là hai đại lượng tỉ lệ thuận với nhau. Với mỗi giá trị \({x_1},{x_2}\) của x, ta có một giá trị tương ứng \({y_1},{y_2}\) của y.
a) Tìm \({x_1}\) biết \({x_2} = 2;{y_1} = - \dfrac{7}{6};{y_2} = - \dfrac{1}{2}\).
b) Tìm \({x_1},{y_1}\) biết \({x_1} - {y_1} = 2;{x_2} = - 4;{y_2} = 3\).
Tìm hai số nguyên dương, biết rằng tổng, hiệu, tích của chúng tỉ lệ thuận với 4; 1; 45.
Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h).
Thay mỗi dấu “?” trong bảng sau bằng số thích hợp.
|
t(h) |
1 |
1,5 |
2 |
3 |
|
s (km) |
? |
? |
? |
? |
Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h).
Viết công thức tính quãng đường s theo thời gian di chuyển tương ứng t.
Trong HĐ 2, quãng đường s có tỉ lệ thuận với thời gian t không? Thời gian t có tỉ lệ thuận với quãng đường s không?
Theo Viện Dinh dưỡng Quốc gia, cứ trong 100 g đậu tương ( đậu nành) thì có 34 g protein. Khối lượng protein trong đậu tương có tỉ lệ thuận với khối lượng đậu tương không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
Cho biết x, y là hai đại lượng tỉ lệ thuận. Thay mỗi dấu “?” trong bảng sau bằng số thích hợp.
|
x |
2 |
4 |
5 |
? |
? |
? |
|
y |
-6 |
? |
? |
9 |
18 |
1,5 |
Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y.
Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không?
Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a, x tỉ lệ thuận với z theo hệ số tỉ lệ b. Hỏi y có tỉ lệ thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu?
Các giá trị của hai đại lượng x và y được cho bởi bảng sau đây:
|
x |
0,5 |
1 |
1,5 |
2 |
2,5 |
|
y |
2,5 |
5 |
7,5 |
10 |
12,5 |
Hỏi hai đại lượng x và y có quan hệ tỉ lệ thuận hay tỉ lệ nghịch không? Viết công thức liên hệ giữa x và y.
Số đo ba góc \(\widehat A,\widehat B,\widehat C\) của tam giác ABC tỉ lệ với 5;6;7. Tính số đo ba góc của tam giác đó.
Cho biết dây điện có giá 10 nghìn đồng một mét. Gọi y (nghìn đồng) là giá tiền của x (mét) dây điện. Hãy tính y theo x.
a) Học sinh trường Nguyễn Huệ tham gia phong trào “Trồng cây xanh bảo vệ môi trường”, mỗi em đều trồng được 4 cây. Gọi c là số cây trồng được, h là số học sinh đã tham gia. Em hãy viết công thức tính c theo h.
b) Tìm điểm giống nhau giữa hai công thức y = 10x và c = 4h.
a) Cho hai đại lượng f và x liên hệ với nhau theo công thức f = 5x. Hãy cho biết đại lượng x có tỉ lệ thuận với đại lượng f hay không. Hệ số tỉ lệ là bao nhiêu?
b) Cho đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8. Hãy viết công thức tính P theo m
Cho biết khối lượng mỗi mét khối của một số kim loại như sau:
Đồng: 8900 kg Vàng: 19300 kg Bạc: 10500 kg
Hãy viết công thức tính khối lượng m (kg) theo thể tích V (\({m^3}\)) của mỗi kim loại và cho biết m tỉ lệ thuận với V theo hệ số tỉ lệ là bao nhiêu.
Cho biết giá trị tương ứng của hai đại lượng x và y tỉ lệ thuận với nhau trong bảng sau:
|
x |
\({x_1}\) = 1 |
\({x_2}\) = 2 |
\({x_3}\) = 6 |
\({x_4}\) = 100 |
|
y |
\({y_1}\)= 5 |
\({y_2}\)= ? |
\({y_3}\)= ? |
\({y_4}\) = ? |
a) Hãy xác định hệ số tỉ lệ của y đối với x
b) Tính các giá trị tương ứng chưa biết của y
c) So sánh các tỉ số giữa hai giá trị tương ứng của y và x
\(\dfrac{{{y_1}}}{{{x_1}}},\dfrac{{{y_2}}}{{{x_2}}},\dfrac{{{y_3}}}{{{x_3}}},\dfrac{{{y_4}}}{{{x_4}}}\)
Trong các trường hợp sau, hãy kiểm tra xem hai đại lượng m và n có tỉ lệ thuận với nhau hay không.
a)
|
m |
2 |
4 |
6 |
8 |
10 |
|
n |
4 |
16 |
36 |
64 |
100 |
b)
|
m |
1 |
2 |
3 |
4 |
5 |
|
n |
-5 |
-10 |
-15 |
-20 |
-25 |
Cho biết hai đại lượng m và n tỉ lệ thuận với nhau. Hãy tìm giá trị của a và b.
|
m |
2 |
3 |
4 |
b |
|
n |
-6 |
-9 |
a |
-18 |
Cho hai đại lượng a và b tỉ lệ thuận với nhau. Biết rằng khi a = 2 thì b = 18.
a) Tìm hệ số tỉ lệ k của a đối với b.
b) Tính giá trị của b khi a = 5.
Cho hai đại lượng x và y tỉ lệ thuận với nhau. Biết rằng khi x = 7 thì y = 21.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x
b) Tìm hệ số tỉ lệ của x đối với y và biểu diễn x theo y
Cho m và n là hai đại lượng tỉ lệ thuận với nhau. Hãy viết công thức tính m theo n và tìm các giá trị chưa biết trong bảng sau:
|
n |
-2 |
-1 |
0 |
1 |
2 |
|
m |
? |
? |
? |
-5 |
? |


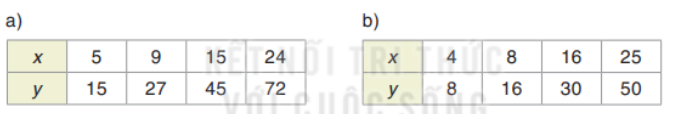






Danh sách bình luận