Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy \(AB = 5 \ cm\) và độ dài trung đoạn \(SI = 6 \ cm\) (hình vẽ bên). Tính:
a) Diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC\)
b) Thể tích của hình chóp \(S.ABC\), biết chiều cao \(SO\) của hình chóp là \(5,8 \ cm\)
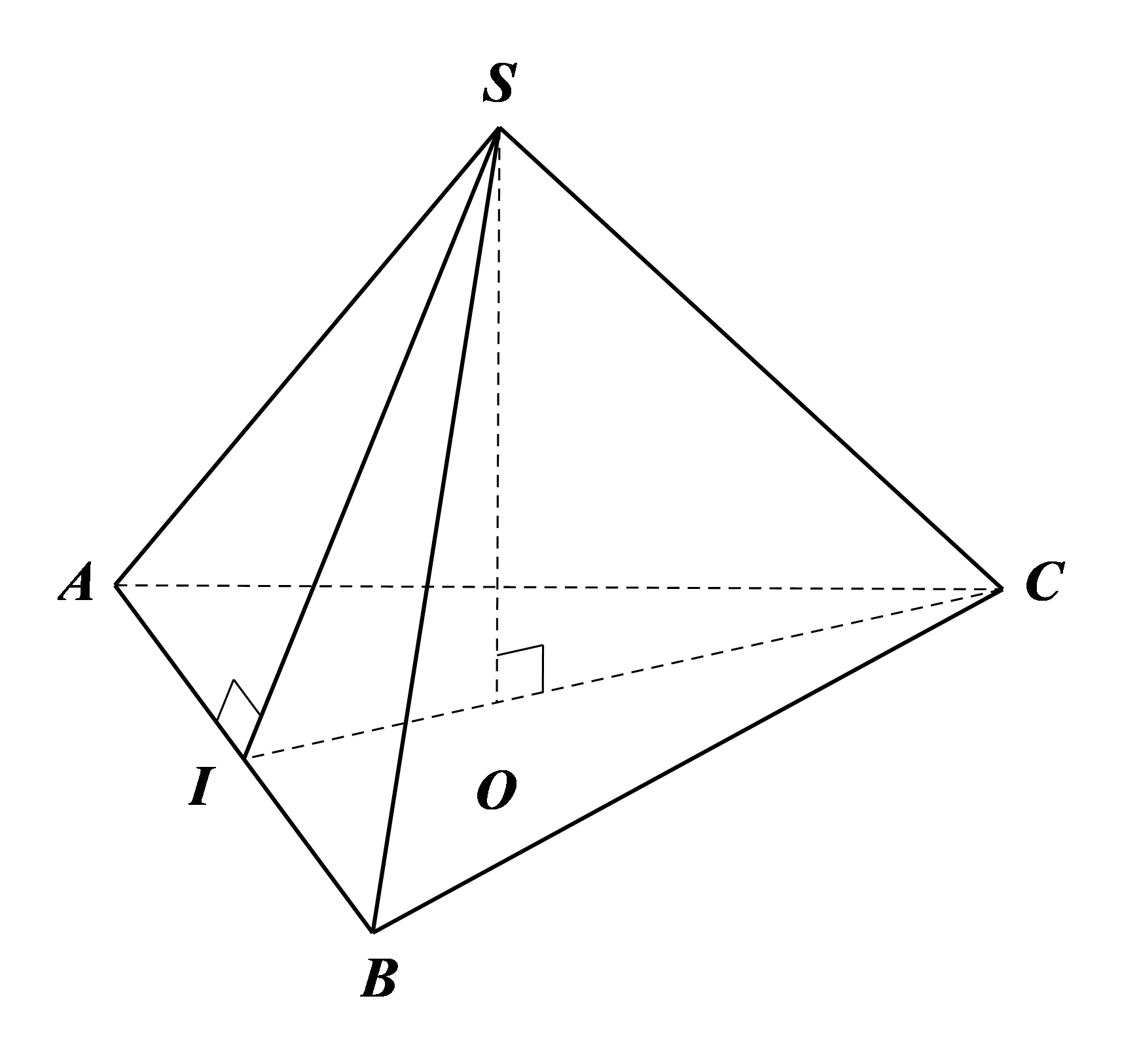
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy \(AB = 5 \ cm\) và độ dài trung đoạn \(SI = 6 \ cm\) (hình vẽ bên). Tính:
a) Diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC\)
b) Thể tích của hình chóp \(S.ABC\), biết chiều cao \(SO\) của hình chóp là \(5,8 \ cm\)
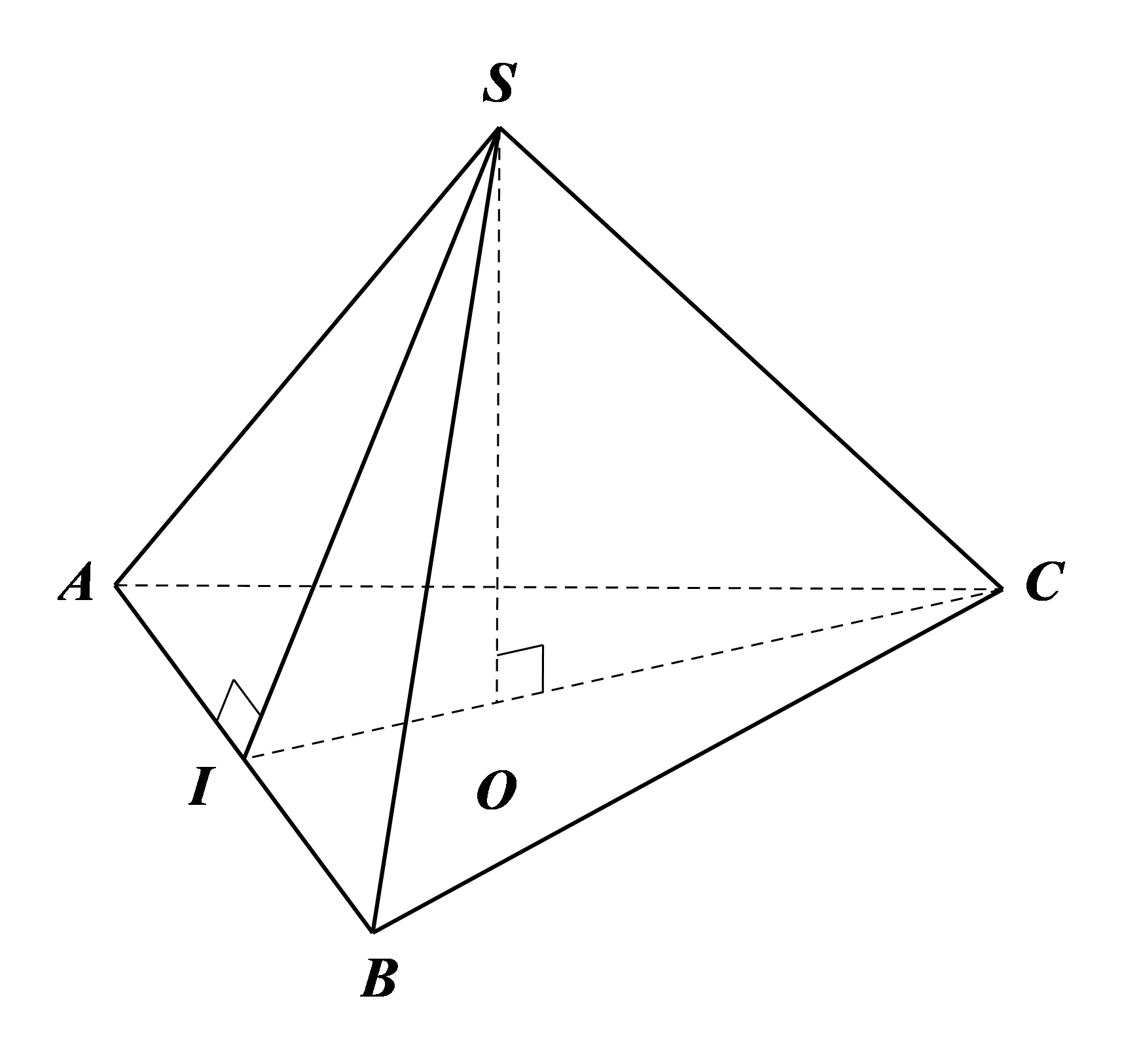
- Công thức tính diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi đáy với trung đoạn.
- Công thức tính diện tích toàn phần bằng diện tích xung quanh hình chóp cộng diện tích đáy.
- Để tính được chiều cao của mặt đáy hình tam giác, ta sử dụng định lí Pythagore.
- Công thức tính thể tích hình chóp tam giác đều bằng \( \frac{1}{3}\) nhân với tích diện tích đáy nhân và chiều cao.
a) Diện tích xung quanh của hình chóp tam giác đều \(S.ABC\) là:
\({S_{xq}} = \frac{1}{2}.\left( {AB + BC + CA} \right).SI = \frac{1}{2}.\left( {5 + 5 + 5} \right).6 = 45\,\left( {c{m^2}} \right)\)
Tam giác \(ABC\) là tam giác đều nên đường trung tuyến \(CI\) đồng thời là đường cao.
Xét \(ΔACI\) vuông tại \(I\) có \(A{C^2} = A{I^2} + C{I^2}\)
Suy ra \(C{I^2} = A{C^2} - A{I^2} = {5^2} - {\left( {\frac{1}{2}.5} \right)^2} = 25 - \frac{{25}}{4} = \frac{{75}}{4}\)
Do đó \(CI = \sqrt {\frac{{75}}{4}} \approx 4,33\,cm\).
Diện tích đáy của hình chóp tam giác đều \(S.ABC\) là:
\(S_{đáy} = \frac{1}{2}.CI.AB \approx \frac{1}{2}.4,33.5 \approx 10,83\,\left( {c{m^2}} \right)\)
Diện tích toàn phần của hình chóp tam giác đều \(S.ABC\) là:
\({S_{tp}} = {S_{xq}} + S_{đáy} \approx 45 + 10,83 = 55,83\,\left( {c{m^2}} \right)\)
b) Thể tích của hình chóp tam giác đều \(S.ABC\) là:
\(V = \frac{1}{3}.SO.S_{đáy} \approx \frac{1}{3}.5,8.10,83 \approx 20,94\,\left( {c{m^3}} \right)\)

Các bài tập cùng chuyên đề
Tính diện tích xung quanh, diện tích toàn phần và thể tích của:
a) Hình chóp tam giác đều có chiều cao là \(98,3\)cm; tam giác đáy có độ dài cạnh là \(40\)cm và chiều cao là \(34,6\)cm; chiều cao mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là \(99\)cm.
b) Hình chóp tứ giác đều có độ dài cạnh đáy là \(120\)cm, chiều cao là \(68,4\)cm, chiều cao mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là \(91\)cm.
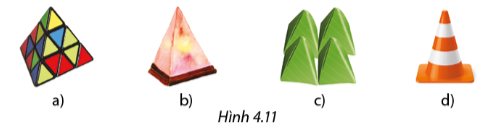
Trong hình 4.11, đồ vật nào có dạng hình chóp tam giác đều, hình chóp tứ giác đều?
Các phát biểu sau đúng hay sai?
a) Hình chóp tam giác đều có tất cả các cạnh bằng nhau;
b) Hình chóp tứ giác đều có đáy là hình vuông.
Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm.
a) Tính độ dài trung đoạn của hình chóp.
b) Tính diện tích xung quanh của chiếc đèn.
c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trần là 1 m là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí A) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?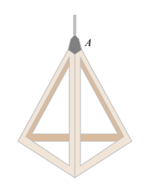
Cho hình chóp tam giác đều S.ABC có SH là đường cao. Phát biểu nào sau đây là sai?
-
A.
Các cạnh bên bằng nhau: SA = SB = SC.
-
B.
\(\Delta ABC\) là tam giác đều.
-
C.
Diện tích xung quanh của hình chóp bằng bốn lần diện tich tam giác SAB.
-
D.
Điểm H là trọng tâm của tam giác ABC.







Danh sách bình luận