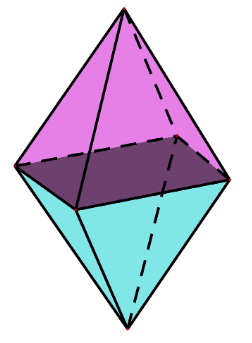
Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy 20 cm, cạnh bên 26 cm, khoảng cách giữa hai đỉnh của hai hình chóp là 30 cm.
a) Tính thể tích của lòng đèn.
b) Bạn Hà muốn dán giấy mờ lên cái lòng đèn hình quả trám này thì cần phải chuẩn bị bao nhiêu mét vuông giấy (bỏ qua các mép dán)?
Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy 20 cm, cạnh bên 26 cm, khoảng cách giữa hai đỉnh của hai hình chóp là 30 cm.
a) Tính thể tích của lòng đèn.
b) Bạn Hà muốn dán giấy mờ lên cái lòng đèn hình quả trám này thì cần phải chuẩn bị bao nhiêu mét vuông giấy (bỏ qua các mép dán)?
Để tính diện tích xung quanh và thể tích hình quả trám, ta chia hình thành hai hình chóp tứ giác đều bằng nhau, sau đó ta nhân 2 để được kết quả.
- Để tính được trung đoạn, ta áp dụng định lý Pythagore.
- Công thức tính diện tích xung quanh hình lăng trụ đứng tứ giác đều: \({S_{xq}} = \frac{1}{2}Cd\).
Trong đó:
+) \({S_{xq}}\) là diện tích xung quanh của hình chóp tứ giác đều.
+) Chu vi đáy : \(C = 4a\) (\(a\) là độ dài cạnh đáy hình vuông).
+) \(d\) là độ dài trung đoạn của hình chóp tứ giác đều.
- Công thức tính thể tích của hình chóp tứ giác đều bằng: \(V = \frac{1}{3}Sh\)
Trong đó:
+) \(V\) là thể tích hình chóp tứ giác đều.
+) S là diện tích đáy.
+) h là chiều cao của khối chóp.
a) Chiều cao của mỗi hình chóp tứ giác đều là \(30:2=15 \ cm\).
Thể tích của lồng đèn quả trám là: \(V = 2.\left( {\frac{1}{3}{{.20}^2}.15} \right) = 4000\,\left( {c{m^3}} \right)\).
b) Một nửa lồng đèn được mô tả bởi hình chóp \(S.ABCD\) với các kích thước như hình vẽ.

Gọi \(M\) là trung điểm của \(BC\) Do đó \(MB=MC= \frac{1}{2}.BC=\frac{1}{2}⋅20=10 \ cm\).
Vì \(ΔSBC\) cân tại \(S\) nên đường trung tuyến \(SM\) đồng thời là đường cao, do đó \(SM \bot BC\) nên \(ΔSBM\) vuông tại M
Áp dụng định lí Pythagore cho \(ΔSBM\) vuông tại \(M\) ta có:
\(S{B^2} = S{M^2} + M{B^2}\)
Suy ra \(S{M^2} = S{B^2} - M{B^2} = {26^2} - {10^2} = 676 - 100 = 576\)
Suy ra \(SM=24 \ cm\).
Diện tích xung quanh (diện tích 4 mặt bên) của hình chóp tứ giác đều là:
\({S_{xq}} = \frac{1}{2}.4.20.24 = 960\,\left( {c{m^2}} \right)\)
Vậy diện tích giấy mờ bạn Hà cần chuẩn bị để làm lồng đèn hình quả trám đó là:
\(S = 2{S_{xq}} = 2.960 = 1920\,\left( {c{m^2}} \right)\)

Các bài tập cùng chuyên đề
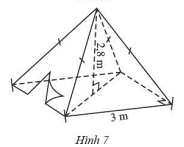
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\)m và lều này không có đáy.
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?
a) Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.
b) Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với chiều cao.
c) Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với độ dài trung đoạn.
d) Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?
a) Nếu độ dài trung đoạn của một hình chóp tứ giác đều tăng lên \(n\) lần \(\left( {n > 1} \right)\) và độ dài cạnh đáy không đổi thì diện tích xung quanh của hình chóp tứ giác đều đó cũng tăng lên \(n\) lần.
b) Nếu độ dài cạnh đáy của một hình chóp tứ giác đều tăng lên \(n\) lần \(\left( {n > 1} \right)\) và chiều cao không đổi thì thể tích của hình chóp tứ giác đều đó cũng tăng lên \(n\) lần.
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m
a) Tính thể tích hình chóp
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31, 92m.
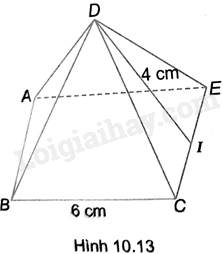
Cho hình chóp tứ giác đều D.ABCE có cạnh đáy bằng 6cm, trung đoạn bằng 4cm như Hình 10.13
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy \(AB = 10cm,\) cạnh bên \(SD = 15cm\). Gọi O là giao điểm của AC và BD, M và N lần lượt là trung điểm của AB và CD.
a) Chứng minh \(SO \bot MN.\) Từ đó tính độ dài đường cao SO của hình chóp.
b) Tính thể tích của hình chóp.
c) Tính diện tích toàn phần của hình chóp.
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 10 cm, trung đoạn bằng 13 cm. (H.10.12).
a) Tính diện tích xung quanh của hình chóp
b) Tính diện tích toàn phần của hình chóp
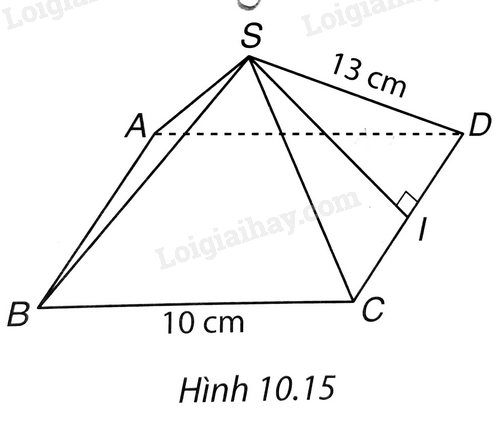
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng 13 cm, cạnh đáy bằng 10 cm như Hình 10.15.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m
a) Tính thể tích hình chóp
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31, 92m.
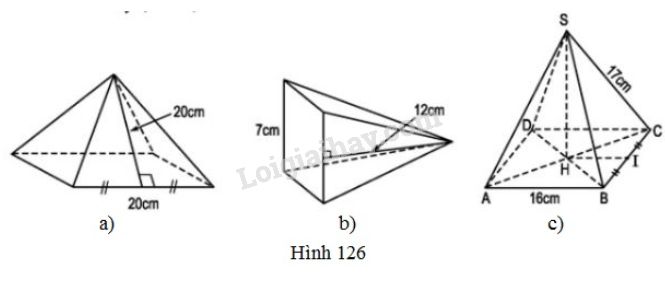
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây.(h.126)







Danh sách bình luận