Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c.
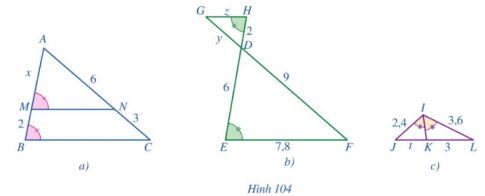
Dựa vào các định lý, tính chất để suy ra tỉ số giữa các cạnh và tính độ dài x, y, z.
a) Xét tam giác AMN và tam giác ABC có:
\(\widehat {AMN} = \widehat {ABC}\) và \(\widehat A\) chung
\( \Rightarrow \Delta AMN \backsim \Delta ABC\)
\(\begin{array}{l} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\\ \Leftrightarrow \frac{x}{{x + 2}} = \frac{6}{{6 + 3}}\\ \Leftrightarrow 9x = 6\left( {x + 2} \right)\\ \Leftrightarrow 9x = 6x + 12\\ \Leftrightarrow x = 4\end{array}\)
b) Vì \(\widehat H = \widehat E\) mà hai góc này so le trong nên \(GH\parallel EF\)
Theo hệ quả của định lý Thales:
\(\begin{array}{l} \Rightarrow \frac{{GH}}{{EF}} = \frac{{GD}}{{FD}} = \frac{{HD}}{{ED}} \Rightarrow \frac{z}{{7,8}} = \frac{y}{9} = \frac{2}{6} = \frac{1}{3}\\ \Rightarrow \frac{z}{{7,8}} = \frac{1}{3} \Rightarrow z = 2,6\\ \Rightarrow \frac{y}{9} = \frac{1}{3} \Rightarrow y = 3\end{array}\)
c) Ta thấy IK là đường phân giác của \(\widehat {LIJ}\)
\( \Rightarrow \frac{{JK}}{{KL}} = \frac{{IJ}}{{IL}} \Rightarrow \frac{t}{3} = \frac{{2,4}}{{3,6}} = \frac{2}{3} \Rightarrow t = 2\)

Các bài tập cùng chuyên đề
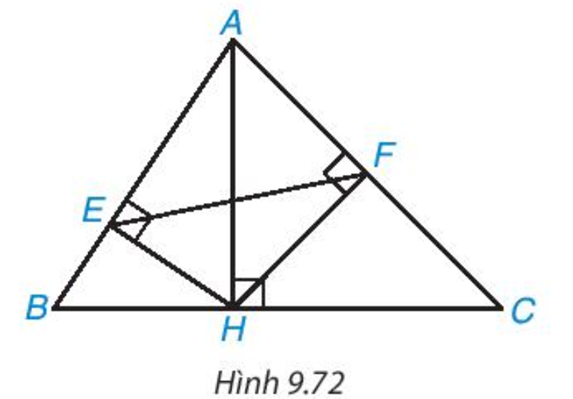
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
a) ΔAEH ∽ ΔAHB
b) ΔAFH ∽ ΔAHC
c) ΔAFE ∽ ΔABC
Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB
a) Chứng minh rằng ΔHDA ∽ ΔAHC
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD
Tính độ dài \(AF\) và \(EF\) trong Hình 6.112.

Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
a) \(HA.HD = HB.HE = HC.HF\);
b) $\Delta AFC\backsim \Delta AEB$ và $AF.AB=AE.AC\,;$
c) $\Delta BDF\backsim \Delta EDC$ và DA là tia phân giác của góc EDF.
Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:
a) $\Delta BDF\backsim \Delta BAC$ và $\Delta CDE\backsim \Delta CAB$;
b) \(BF.BA + CE.CA = B{C^2}\)
Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H). Kẻ đường thẳng qua M vuông góc với BC lần lượt cắt AC và tia đối của tia AB tại N và P. Chứng minh rằng:
a) $\Delta ANP\backsim \Delta HBA$ và $\Delta MCN\backsim \Delta MPB$;
b) \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = 1\)
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:
a) \(AM.AB = A{H^2}\) và \(AM.AB = AN.AC\)
b) $\Delta AMN\backsim \Delta ACB$
Cho ABC và A’B’C’ lần lượt là các tam giác vuông tại đỉnh A và A’. Gọi M, M’ lần lượt là trung điểm của AC và A’C’. Chứng minh rằng:
a) \(B{C^2} + 3B{A^2} = 4B{M^2}\) và \(B'C{'^2} + 3B'A{'^2} = 4B'M{'^2}\);
b) Nếu \(\frac{{BC}}{{BM}} = \frac{{B'C'}}{{B'M'}}\) thì $\Delta ABC\backsim \Delta A'B'C'$.
Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.
a) Chứng minh rằng \(CM \bot DN\).
b) Biết \(AB = 4cm,\) hãy tính diện tích tam giác ONC.
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:
a) $\Delta MNP\backsim \Delta ABC$ và tìm tỉ số đồng dạng
b) $\Delta ABN\backsim \Delta CAM$ và $\Delta ACP\backsim \Delta BAM$
c) \(AN \bot CM\) và \(AP \bot BM\)
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng $\Delta CAM\backsim \Delta CBN$ và $\Delta CHM\backsim \Delta CAN$
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB.
a) Chứng minh ΔBMP ∽ ΔMCN
b) Tính độ dài đoạn thẳng AM
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là các điểm trên các đoạn thẳng AB, AH sao cho AM = 2.MB, AN = $\frac{1}{2}$NH.
Chứng minh rằng $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$.
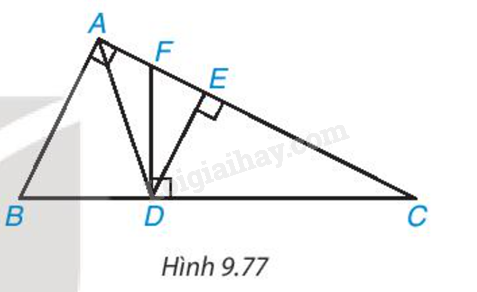
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC. Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\);
b) ΔDFC ∽ ΔABC;
c) DF = DB
Cho tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\) Lấy điểm D trên cạnh BC sao cho \(BD = 2cm.\) Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.
a) Chứng minh rằng $\Delta BDE\backsim \Delta DCF$
b) Tính độ dài đoạn thẳng AD.
Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cm. Trên cạnh AC lấy điểm D sao cho CD = 4cm, trên cạnh BC lấy điểm M sao cho BM = 10cm. Kẻ đoạn thẳng MD.
a) Chứng tỏ rằng DM // AB.
b) Chứng minh $\Delta BAC\backsim \Delta MDC$.
c) Xác định tỉ số giữa diện tích của tam giác MDC với diện tích tam giác ABC.
Cho \(\Delta ABC\) có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\). Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\).
a) $\Delta ABD\backsim \Delta ACB$.
b) \(\widehat {ADB} = \widehat {ABC}\).
c) \(AD = 0,5cm,DC = 3,5cm\).
d) \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
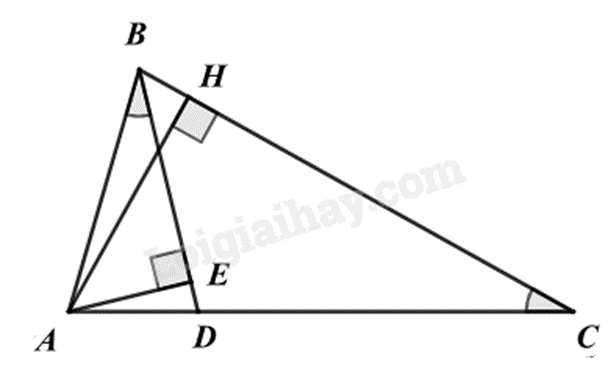
Cho \(\Delta ABC\) vuông tại A có \(AB = 6cm\) và \(AC = 8cm\). Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ \(CE \bot BD\) kẻ E.
a) Tính độ dài BC và tỉ số \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$. Từ đó suy ra \(BD.EC = AD.BC\).
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\).
d) Gọi EH là đường cao của \(\Delta EBC\). Chứng minh \(CH.CB = ED.EB\).
Cho tam giác ABC (AB < AC) vuông tại A có đường cao AH.
a) Chứng minh rằng $\Delta ABC\backsim \Delta HAC$.
b) Lấy điểm I thuộc đoạn AH (I không trùng với A, H). Qua B kẻ đường thẳng vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\).
c) Tia BK cắt tia HA tại điểm D. Chứng minh \(CH.CB + DK.DB = C{D^2}\).
Cho hình chữ nhật ABCD. Kẻ \(AH \bot BD\) tại H.
a) Chứng minh rằng $\Delta ABD\backsim \Delta HBA$.
b) Chứng minh rằng \(B{C^2} = BD.DH\).
c) Kẻ DE là đường phân giác của tam giác ABD. Gọi I là giao điểm của DE và AH. Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB\).
Cho tam giác ABC cân tại A có đường cao AM, N là trung điểm của AC. Kẻ Ax // BC, cắt MN tại E.
a) M là trung điểm của BC.
b) ME // AB.
c) AE = MC.
d) $\Delta AEN\backsim \Delta CNM$.
Cho hình vuông ABCD cạnh a, điểm E thuộc cạnh BC, điểm F thuộc cạnh AD sao cho CE = AF. Các đường thẳng AE, BF cắt đường thẳng CD theo thứ tự ở M và N.
1. Chứng minh \(CM.DN=a^2\)
2. Gọi K là giao điểm của NA và MB. Chứng minh \(\widehat{MKN}=90^\circ\).







Danh sách bình luận