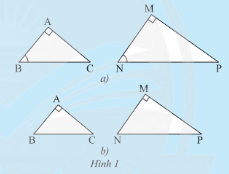
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\widehat B = \widehat N\) thì hai tam giác đó có đồng dạng với nhau không.
b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) thì hai tam giác đó có đồng dạng với nhau không.
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\widehat B = \widehat N\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)
b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).

Các bài tập cùng chuyên đề
Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng?
a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
b) Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.
c) Hai góc của tam giác này bằng hai góc của tam giác kia.
d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)
a) Chứng minh rằng ΔABN ∽ ΔACM
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM
Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM ∽ ΔHAN
Tam giác \(ABC\) có độ dài \(AB = 4cm,AC = 6cm,BC = 9cm.\) Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác \(A'B'C'\).
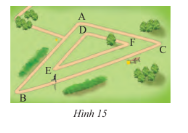
Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 600 m. Nam chạy bốn vòng bên trong. Hưng chạy hai vòng bên ngoài. So sánh quãng đường chạy của hai bạn.
Cho tam giác \(ABC\) nhọn có hai đường cao \(BM,CN\) cắt nhau tại \(H\).
a) Chứng minh rằng \(\Delta AMN\backsim\Delta ABC\).
b) Phân giác của \(\widehat {BAC}\) cắt \(MN\) và \(BC\) lần lượt tại \(I\) và \(K\). Chứng minh rằng \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\).
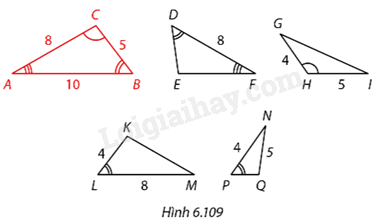
Trong Hình 6.109, các tam giác nào đồng dạng với tam giác \(ABC?\)
Cho \(\Delta ABC\) có \(AB = 9cm,AC = 12cm\) và \(BC = 15cm.\) Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(AM = 4cm\) và trên cạnh \(AB\) lấy điểm \(N\) sao cho \(AN = 3cm\) . Gọi \(O\) là giao điểm của \(CM\) và \(BN\) . Chứng minh rằng:
a) \(\Delta ABN ∽ \Delta ACM;\)
b) \(\Delta BMO ∽ \Delta CNO;\)
c) \(\Delta BOC ∽ \Delta MON;\)
d) \(CM\) là tia phân giác của góc \(ACB\) và \(\Delta MBN\) cân tại \(M.\)
Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho \(\widehat {APQ} = \widehat {ACB}\). Chứng minh rằng:
a) \(AP.AB = AQ.AC\)
b) $\Delta APC\backsim \Delta AQB$
Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}.\) Gọi O là giao điểm của BN và CM. Chứng minh rằng:
a) \(AM.AB = AN.AC\)
b) \(OM.OC = ON.OB\)
Câu nào sau đây là sai?
A. Hai tam giác có các cặp cạnh tương ứng tỉ lệ thì có các cặp góc tương ứng bằng nhau.
B. Hai tam giác có hai cặp góc tương ứng bằng nhau thì có cặp cạnh tương ứng tỉ lệ.
C. Hai tam giác có một cặp góc tương ứng bằng nhau và hai cặp cạnh tương ứng tỉ lệ thì đồng dạng với nhau.
D. Hai tam giác cùng đồng dạng với một tam giác theo cùng một tỉ số đồng dạng thì bằng nhau.
Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng?
a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
b) Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.
c) Hai góc của tam giác này bằng hai góc của tam giác kia.
d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.
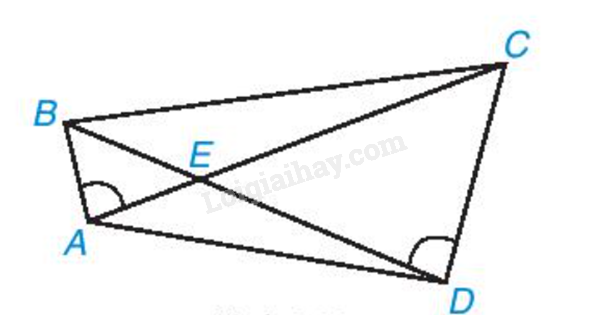
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Cho tam giác ABC cân tại A và M là trung điểm của cạnh BC. Lấy các điểm D, E lần lượt trên các cạnh AB, AC sao cho $\widehat{DME}=\widehat{ABC}$.
a) Chứng minh $\Delta BDM\backsim \Delta CME$.
b) Chứng minh DM là phân giác của góc BDE.
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Các đường thẳng qua E, F lần lượt vuông góc và cắt CH, BH tại P, Q. Chứng minh rằng PQ // BC và $\Delta HPQ\backsim \Delta HEF$.
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh $\Delta ABC\backsim \Delta HBA$.
b) Tia phân giác của góc AHC cắt AC tại D. Chứng minh \(\frac{{HB}}{{HC}} = \frac{{A{D^2}}}{{D{C^2}}}\).







Danh sách bình luận