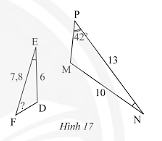
Trong Hình 17, cho biết $DE = 6cm,EF = 7,8cm,NP = 13cm,NM = 10cm,\widehat E = \widehat N$ và $\widehat P = 42^\circ$. Tính $\widehat F$.

 

Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?

Cho hình thoi ABCD cạnh a, có $\hat A = {60^0}$ . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính $\widehat {BKD}$ .

Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

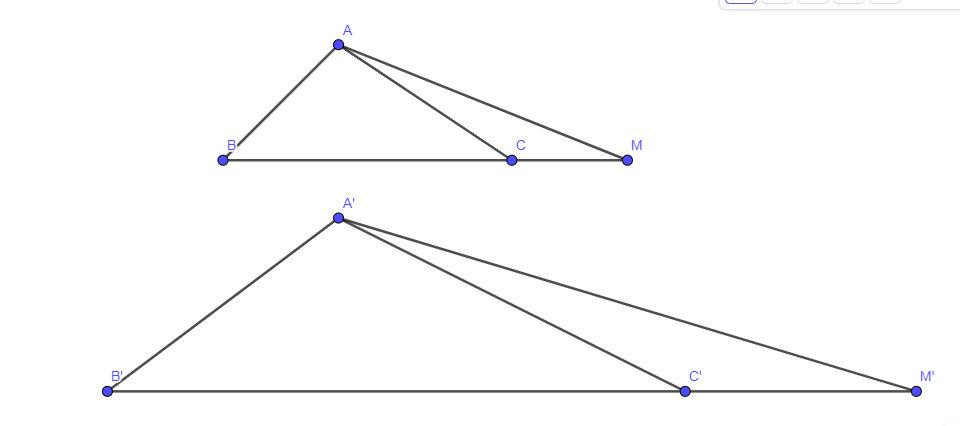
Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho $\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}$. Chứng minh rằng  ΔA'B'M' ∽ ΔABM

Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có $\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}$ và $\widehat {B'} = \widehat B$ thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?

Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho $\Delta AMC$ cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.

Cho tam giác ABC có AB=12cm, AC=15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM=10cm, AN=8cm. Chứng minh rằng ΔABC ∽ ΔANM.

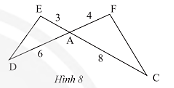
Cho tam giác $ADE$ và tam giác $ACF$ có các kích thước như trong Hình 8. Chứng minh rằng $\Delta ADE\backsim\Delta ACF$.

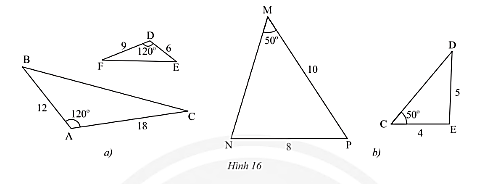
Xét xem cặp tam giác nào trong Hình 16a,16b đồng dạng?

a) Cho tam giác $ABC$ có $AB = 12cm,AC = 15cm,BC = 18cm$. Trên cạnh $AB$, lấy điểm $E$ sao cho $AE = 10cm$. Trên cạnh $AC$, lấy điểm $F$ sao cho $AF = 8cm$ (hình 18a). Tính độ dài đoan thẳng $EF$.

b) Trong Hình 18b, cho biết $FD = FC,BC = 9dm,DE = 12dm,AC = 15dm,MD = 20dm.$

Chứng minh rằng $\Delta ABC\backsim\Delta MED$.

Quan sát hình 68 và so sánh:

a) Các tỉ số $\frac{{A'B'}}{{AB}}$ và $\frac{{A'C'}}{{AC}}$

b) Các góc $\widehat A$ và $\widehat {A'}$

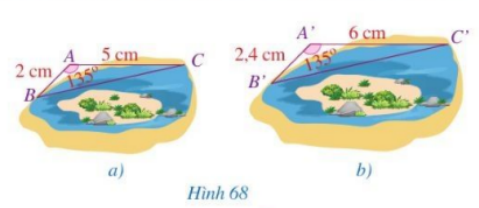
Cho hai tam giác ABC và A’B’C’ thỏa mãn $AB = 2,AC = 3,A'B' = 6,A'C' = 9$ và $\widehat A = \widehat {A'}$. Chứng minh $\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}$.

Cho góc $xOy$. Trên tia Ox lấy các điểm A, B sao cho $OA = 2cm,\,\,OB = 9cm$. Trên tia Oy lấy các điểm M, N sao cho $OM = 3cm,\,\,ON = 6cm$. ChỨNG minh $\widehat {OBM} = \widehat {ONA}$.

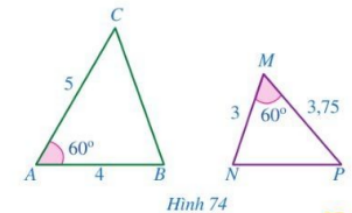
Cho Hình 74.

a) Chứng minh $\Delta ABC \backsim \Delta MNP$

b) Góc nào của tam giác MNP bằng góc B?

c) Góc nào của tam giác ABC bằng góc P?

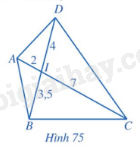
Cho Hình 75, chứng minh:

a) $\Delta IAB \backsim \Delta IDC$

b) $\Delta IAD \backsim \Delta IBC$

Cho $\Delta ABC \backsim \Delta MNP$.

a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh $\Delta ABD \backsim \Delta MNQ$.

b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh $\Delta ABG \backsim \Delta MNK$.

Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thỏa mãn $AB = 20m,{\rm{ }}AC = 50m,\;\,\,\widehat {BAC} = 135^\circ$

Bạn Vy làm như sau: Vẽ tam giác A'B'C' có $A'B' = 2cm,{\rm{ }}A'C' = 5cm,\;\widehat {B'A'C'} = 135^\circ$. Bạn Vy lấy thước đo khoảng cách giữa hai điểm B', C' và nhận được kết quả $B'C'\; \approx \;6,6cm$. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.

Cho hai tam giác ABC và PMN thỏa mãn $\widehat A = 70^\circ ,\,\,\widehat B = 80^\circ ,\,\,\widehat M = 80^\circ ,\,\,\widehat N = 30^\circ$. Chứng minh $\frac{{AB}}{{PM}} = \frac{{BC}}{{MN}} = \frac{{CA}}{{NP}}$.

Cắt $\Delta A'B'C'$ và $\Delta ABC$ bằng tờ giấy có $\widehat {A'} = \widehat A$ và $\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}.$ Xếp $\Delta A'B'C'$ và $\Delta ABC$ sao cho cạnh $A'B'$ chồng lên cạnh $AB$ và cạnh $A'C'$ chồng lên cạnh $AC$ như Hình 6.59.

1. Vì sao trong Hình $6.59b$ cạnh $B'C'$ song song với cạnh $BC?$

2. Em có kết luận gì về $\Delta A'B'C'$ và $\Delta ABC$?

Khẳng định nào sau đây đúng với các tam giác trong Hình 6.22?

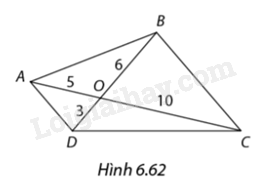
a) $\Delta AOD \backsim \Delta COB;$

b) $\Delta AOB \backsim \Delta DOC.$

Xác định các cặp tam giác đồng dạng với nhau trong Hình 6.65. Cho biết kí hiệu của sự đồng dạng và xác định tỉ số đồng dạng trong mỗi trường hợp.

Bạn Cường đo được khoảng cách từ vị trí mình đứng (điểm C) đến cây A và  cây B ở hai bên hồ nước lần lượt là $AC = 24m$ và $BC = 28m$ (Hình 6.66). Để tính độ dài $AB,$ Cường xác định điểm $D$ nằm giữa $A,C$ và điểm $E$ nằm giữa $B,C$ sao cho $CD = 6m,CE = 7m$ và đo khoảng cách giữa $D$ và $E.$ Nếu $DE = 9m$ thì khoảng cách giữa $A$ và $B$ là bao nhiêu mét?

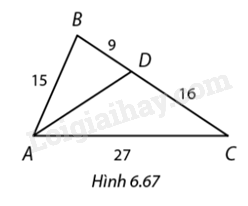
Chứng minh rằng trong Hình 6.67, $\Delta ABC \backsim \Delta DBA.$ Tính độ dài đoạn thẳng $AD.$

Giải thích vì sao trong Hình 6.76, $\Delta A'B'C'$ đồng dạng với $\Delta ABC$?

Cho $\Delta ABC$ có $AD$ là đường trung tuyến. Một đường thẳng $d$ song song với $BC$ cắt $AB,AC$ và $AD$ lần lượt tại $M,N$ và $O$ .

a) Chứng minh rằng $O$ là trung điểm của $MN.$

b) Cho tỉ số của diện tích $\Delta AMN$ và $\Delta ABC$ là $\frac{4}{9}$ . Chứng minh rằng $O$ là trọng tâm của $\Delta ABC.$ 

Với hai tam giác ABC và DEF bất kì thỏa mãn $\frac{{AB}}{{EF}} = \frac{{BC}}{{DF}},\widehat {ABC} = \widehat {DFE}$. Những khẳng định nào sau đây là đúng?

(1) $\Delta ABC\backsim \Delta DEF$

(2) $\Delta CAB\backsim \Delta DEF$

(3) $\Delta ABC\backsim \Delta EFD$

(4) $\Delta BCA\backsim \Delta EFD$

(5) $\Delta ABC\backsim \Delta FDE$

(6) $\Delta BAC\backsim \Delta FED$

Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho $AM.AB = AN.AC$.

a) Chứng minh rằng $\Delta AMN\backsim \Delta ACB$

b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng $\widehat {EAB} = \widehat {FAC}$

Cho hình thang ABCD (AB//CD). Biết rằng $AB = 2cm,BD = 4cm,CD = 8cm.$ Chứng minh rằng $BC = 2AD$

Cho tam giác ABC với $AB = 6cm,AC = 9cm.$ Lấy điểm D trên cạnh AC sao cho $AD = 4cm.$ Chứng minh rằng $\Delta ABD\backsim \Delta ACB$ và $BC = \frac{3}{2}BD$

Cho tứ giác ABCD như hình 9.6. Biết rằng $AB = 2cm,AC = 4cm,AD = 8cm$ và AC là phân giác của góc BAD. Chứng minh $CD = 2BC$

Hình 9.6

Cho tam giác ABC với $AB > AC$. Lấy điểm D trên cạnh AB sao cho $AC = AD$. Qua D kẻ đường thẳng song song với BC và cắt AC tại E. Qua E kẻ đường thẳng song song với CD và cắt AB tại F. Chứng minh rằng:

a) $A{D^2} = AF.AB$

b) $\Delta ACF\backsim \Delta ABC$