Bảng dưới đây tổng hợp thời gian hoàn thành bài kiểm tra IQ của 50 học sinh lớp 9:

Tính trung bình và độ lệch chuẩn của mẫu số liệu đã cho. Nêu ý nghĩa của kết quả tìm được.
Áp dụng các công thức tính trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm:
- Công thức tính trung bình là
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{c_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Kích thước của mẫu số liệu là N = 50.
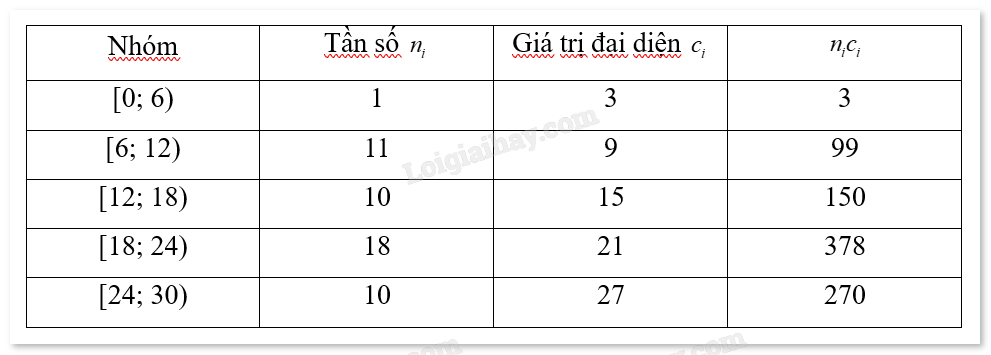
Vì có 5 nhóm nên k = 5. Trung bình mẫu:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{3 + 99 + 150 + 378 + 270}}{{50}} = 18\)
Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2} = \frac{{1.{{(3 - 18)}^2} + 11.{{(9 - 18)}^2} + 10.{{(15 - 18)}^2} + 18.{{(21 - 18)}^2} + 10.{{(27 - 18)}^2}}}{{50}} = \frac{{1089}}{{25}} = 43,56\)
Độ lệch chuẩn là:
\(S = \sqrt {{S^2}} = \sqrt {43,56} = 6,6\)
Các kết quả vừa tìm được cho thấy thời gian làm bài kiểm tra IQ của các học sinh lớp 9 có sự chênh lệch khoảng 6,6 so với thời gian trung bình.

Các bài tập cùng chuyên đề
Một nhóm 20 học sinh dùng một thiết bị đo đường kính của một nhân tế bào cho kết quả như sau:
a) Tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Số trung bình và độ lệch chuẩn cho biết thông tin gì?
Thời gian chạy tập luyện cự li 100m của hai vận động viên được cho trong bảng sau: 
Dựa trên độ lệch chuẩn của mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.
Có nên dùng phương sai (hoặc độ lệch chuẩn) để so sánh độ phân tán của hai mẫu số liệu ghép nhóm trong mỗi trường hợp sau không? Tại sao?
a) Các mẫu số liệu ghép nhóm về điểm thi tốt nghiệp môn Toán của học sinh hai trường trung học phổ thông có chất lượng tương đương.
b) Các mẫu số liệu ghép nhóm về doanh thu của 100 cửa hàng bán lẻ và doanh thu của 100 siêu thị.
Có nên dùng phương sai (hoặc độ lệch chuẩn) để so sánh độ phân tán của hai mẫu số liệu ghép nhóm trong mỗi trường hợp sau không? Tại sao?
a) Các mẫu số liệu ghép nhóm về điểm thi tốt nghiệp môn Toán của học sinh hai trường trung học phổ thông có chất lượng tương đương.
b) Các mẫu số liệu ghép nhóm về doanh thu của 100 cửa hàng bán lẻ và doanh thu của 100 siêu thị.
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau: 
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả số đo của An và Bình. Từ đó kết luận xem vôn kết của bạn nào cho kết quả ổn định hơn.
Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng)

a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A,B
b) Công ty nào có mức lương đồng đều hơn?
Mai và Ngọc cùng sử dụng vòng đeo tay thông minh để ghi lại số bước chân hai bạn đi mỗi ngày trong một tháng. Kết quả được ghi lại ở bảng sau:

a) Hãy tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Nếu so sánh theo độ lệch chuẩn thì bạn nào có số lượng bước chân đi mỗi ngày đều đặn hơn?
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:

a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B.
b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây?
-
A.
Số trung bình
-
B.
Số trung vị
-
C.
Mốt
-
D.
Phương sai
Khẳng định nào sau đây sai?
-
A.
Khoảng biến thiên và khoảng tứ vị phân càng lớn thì mẫu số liệu càng phân tán.
-
B.
Phương sai và độ lệch chuẩn càng lớn thì thì mẫu số liệu càng phân tán.
-
C.
Khoảng biến thiên sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng.
-
D.
Khoảng tứ phân vị sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng.
Độ lệch chuẩn của mỗi mẫu số liệu ghép nhóm sau đây cho biết điều gì?
a) Mẫu số liệu ghép nhóm về thành tích 20 lần luyện tập (đơn vị tính là phút) của một vận động viên chạy cự li 1 000 mét.
b) Mẫu số liệu ghép nhóm về kết quả 20 lần đo khoảng cách từ Trái Đất đến một ngôi sao (đơn vị là năm ánh sáng) khi dùng một thiết bị đo mới được chế tạo.
Chị Yến thống kê lại thời gian chạy cự li 200 m của mình ở một số lần luyện tập trong năm 2022 và 2023 như sau:
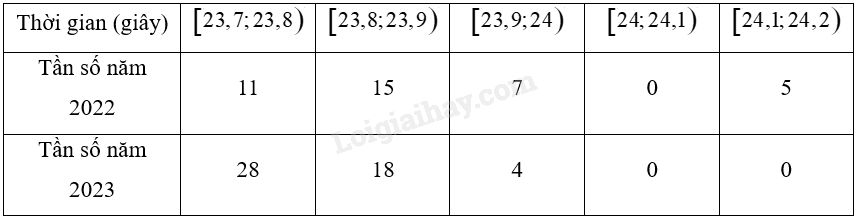
a) Hãy tính các số đặc trưng đo mức độ phân tán thời gian chạy mỗi năm của chị Yến (kết quả làm tròn đến hàng phần nghìn).
b) Độ phân tán của mẫu số liệu cho biết điều gì?
Bộ phận kiểm tra chất lượng sản phẩm dùng máy để đo (chính xác đến 0,001 mm) độ dày của một chi tiết máy. Kết quả đo một số sản phẩm được thống kê trong bảng sau:

a) Tính phương sai và độ lệch chuẩn của độ dày chi tiết máy.
b) Giải thích tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này.
Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:

a) Ước tính giá trị trung bình và độ lệch chuẩn của đường kính các ổ bi được sản xuất bởi mỗi máy.
b) Biết rằng đường kính mong muốn cho các ổ bi là 30,4 mm. Hãy phân tích chất lượng sản phẩm do mỗi máy sản xuất.
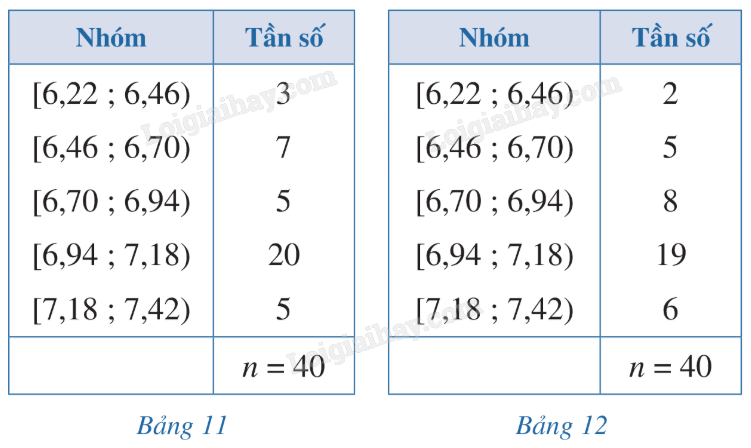
Kết quả 40 lần nhảy xa của hai vận động viên nam Dũng và Huy được lần lượt thống kê trong Bảng 11 và Bảng 12 (đơn vị: mét). Kết quả nhảy xa của vận động viên nào đồng đều hơn?







Danh sách bình luận