Phát biểu nào sau đây là đúng?

A. \(\int\limits_a^b {\cos xdx}  = \sin a - \sin b\).

B. \(\int\limits_a^b {\cos xdx}  = \sin b - \sin a\).

C. \(\int\limits_a^b {\cos xdx}  = \cos a - \cos b\).

D. \(\int\limits_a^b {\cos xdx}  = \cos b - \cos a\).

Tính tích phân \(\int\limits_2^3 {\frac{1}{{{x^2}}}} dx\) có giá trị bằng:

A. \(\frac{1}{6}\)

B. \( - \frac{1}{6}\)

C. \(\frac{{19}}{{648}}\)

D. \( - \frac{{19}}{{648}}\)

Tích phân \(\int\limits_{\frac{\pi }{7}}^{\frac{\pi }{5}} {\sin xdx} \) có giá trị bằng:

Tích phân \(I = \int\limits_0^1 {\frac{{{3^x}}}{2}dx} \) có giá trị bằng:

A. \( - \frac{1}{{\ln 3}}\)

B. \(\frac{1}{{\ln 3}}\)

C. -1

D. 1

Tính:

a) \(\int\limits_0^1 {({x^6} - 4{x^3} + 3{x^2})dx} \)

b) \(\int\limits_1^2 {\frac{1}{{{x^4}}}dx} \)

c) \(\int\limits_1^4 {\frac{1}{{x\sqrt x }}dx} \)

d) \(\int\limits_0^{\frac{\pi }{2}} {(4\sin x + 3\cos x)dx} \)

e) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {{{\cot }^2}xdx} \)

g) \(\int\limits_0^{\frac{\pi }{4}} {{{\tan }^2}xdx} \)

h) \(\int\limits_{ - 1}^0 {{e^{ - x}}dx} \)

i) \(\int\limits_{ - 2}^{ - 1} {{e^{x + 2}}dx} \)

k) \(\int\limits_0^1 {({{3.4}^x} - 5{e^{ - x}})dx} \)

a) Cho một vật chuyển động với vận tốc y = v(t) (m/s). Cho 0 < a < b và v(t) > 0 với mọi \(t \in [a;b]\). Hãy giải thích vì sao \(\int\limits_a^b {v(t)dt} \) biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b (a,b tính theo giây)

b) Áp dụng công thức ở câu a) để giải bài toán sau: một vật chuyển động với vận tốc v(t) = 2 – sint (m/s). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm t = 0 (s) đến thời điểm \(t = \frac{{3\pi }}{4}\) (s)

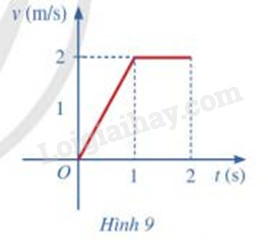
Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9.

a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên

b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên

Ở nhiệt độ \(37^\circ C\), một phản ứng hóa học từ chất đầu A, chuyển hóa thành sản phẩm B theo phương trình: \(A \to B\). Giả sử y(x) là nồng độ chất A (đơn vị mol \({L^{ - 1}}\)) tại thời gian x (giây), y(x) > 0 với \(x \ge 0\), thỏa mãn hệ thức \(y'(x) =  - {7.10^{ - 4}}y(x)\) với \(x \ge 0\). Biết rằng tại x = 0, nồng độ (đầu) của A là 0,05 mol \({L^{ - 1}}\).

a) Xét hàm số \(f(x) = \ln y(x)\) với \(x \ge 0\). Hãy tính f’(x), từ đó hãy tìm hàm số f(x)

b) Giả sử tính nồng độ trung bình chất A (đơn vị mol \({L^{ - 1}}\)) từ thời điểm a(giây) đến thời điểm b(giây) với 0 < a < b theo công thức \(\frac{1}{{b - a}}\int\limits_a^b {y(x)dx} \). Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây.

Tính các tích phân sau:

a) \(\int\limits_1^2 {{x^4}dx} \)

b) \(\int\limits_1^2 {\frac{1}{{\sqrt x }}dx} \)

c) \(\int\limits_0^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx} \)

d) \(\int\limits_0^2 {{3^x}dx} \)

Tính các tích phân sau:

a) \(\int\limits_0^1 {{{\left( {1 - 2x} \right)}^2}dx} \);

b) \(\int\limits_1^4 {\frac{{x - 2}}{{\sqrt x }}dx} \).

Tính các tích phân sau:

a) \(\int\limits_0^2 {\left| {2x - 1} \right|dx} \);

b) \(\int\limits_{ - 2}^3 {\left| {x - 1} \right|dx} \).

Tính các tích phân sau:

a) \(\int\limits_0^{\frac{\pi }{2}} {\left( {3\cos x + 2\sin x} \right)dx} \);

b) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).

Tính các tích phân sau:

a) \(\int\limits_0^1 {\left( {{3^x} - 2{e^x}} \right)dx} \);

b) \(\int\limits_0^1 {\frac{{{{\left( {{e^x} - 1} \right)}^2}}}{{2{e^x}}}dx} \).

Phát biểu nào sau đây là đúng?

A. \(\int\limits_a^b {\sin xdx}  = \sin a - \sin b\).

B. \(\int\limits_a^b {\sin xdx}  = \sin b - \sin a\).

C. \(\int\limits_a^b {\sin xdx}  = \cos a - \cos b\).

D. \(\int\limits_a^b {\sin xdx}  = \cos b - \cos a\).

Phát biểu nào sau đây là đúng? Biết \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}}\) liên tục trên \(\left[ {a;b} \right]\).

A. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx}  = \cot a - \cot b\).

B. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx}  = \cot b - \cot a\).

C. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx}  = \tan a - \tan b\).

D. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx}  = \tan b - \tan a\).

Tích phân \(\int\limits_1^2 {\frac{{ - 3}}{{{x^3}}}dx} \) có giá trị bằng:

A. \(\frac{9}{8}\).

B. \( - \frac{{45}}{{64}}\).

C. \(\frac{{15}}{8}\).

D. \( - \frac{9}{8}\).

Tích phân \(\int\limits_1^2 {\frac{1}{{x\sqrt x }}dx} \) có giá trị bằng:

A. \(2 - \sqrt 2 \).

B. \(2 + \sqrt 2 \).

C. \(\frac{{ - \sqrt 2  + 8}}{{20}}\).\

D. \(\frac{{ - \sqrt 2  - 8}}{{20}}\).

Phát biểu nào sau đây là đúng? Biết \(f\left( x \right) = \frac{1}{{{{\cos }^2}x}}\) liên tục trên \(\left[ {a;b} \right]\).

A. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx}  = \cot a - \cot b\).

B. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx}  = \cot b - \cot a\).

C. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx}  = \tan a - \tan b\).

D. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx}  = \tan b - \tan a\).

Cho \(m\) thoả mãn \(m > 0,m \ne 1\). Phát biểu nào sau đây là đúng?

A. \(\int\limits_a^b {{m^x}dx}  = {m^b} - {m^a}\).

B. \(\int\limits_a^b {{m^x}dx}  = {m^a} - {m^b}\).

C. \(\int\limits_a^b {{m^x}dx}  = \frac{{{m^b}}}{{\ln m}} - \frac{{{m^a}}}{{\ln m}}\).

D. \(\int\limits_a^b {{m^x}dx}  = \frac{{{m^a}}}{{\ln m}} - \frac{{{m^b}}}{{\ln m}}\).

Tính:

a) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} \);

b) \(\int\limits_0^{\frac{\pi }{4}} {\cos xdx} \);

c) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{1}{{{{\sin }^2}x}}dx} \);

d) \(\int\limits_0^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx} \);

e) \(\int\limits_0^{\frac{\pi }{2}} {\left( {\sin x - 2} \right)dx} \);

g) \(\int\limits_0^{\frac{\pi }{4}} {\left( {3\cos x + 2} \right)dx} \).

Tính:

a) \(\int\limits_0^2 {{e^{ - 5{\rm{x}}}}dx} \);

b) \(\int\limits_0^1 {{3^{x + 2}}dx} \);

c) \(\int\limits_{ - 1}^1 {{3^{2{\rm{x}}}}dx} \).

Tính:

a) \(\int\limits_0^1 { - 2dx} \);

b) \(\int\limits_0^1 {\frac{{2x}}{3}dx} \);

c) \(\int\limits_0^1 {{x^4}dx} \);

d) \(\int\limits_1^3 {2\sqrt[3]{x}dx} \);

e) \(\int\limits_1^2 {\frac{2}{{3x}}dx} \);

g) \(\int\limits_1^9 {\left( {x\sqrt x  - 2} \right)dx} \).

Tính các tích phân sau:

a) \(\int\limits_0^2 {\left( {3x - 2} \right)\left( {3x + 2} \right)dx} \);

b) \(\int\limits_1^2 {{t^2}\left( {5{t^2} - 2} \right)dt} \);

c) \(\int\limits_{ - 1}^1 {\left( {x - 2} \right)\left( {{x^2} + 2{\rm{x}} + 4} \right)dx} \).

Tính các tích phân sau:

a) \(\int\limits_1^2 {\frac{{1 - 2{\rm{x}}}}{{{x^2}}}dx} \);

b) \(\int\limits_1^2 {{{\left( {\sqrt x  + \frac{1}{{\sqrt x }}} \right)}^2}dx} \);

c) \(\int\limits_1^4 {\frac{{x - 4}}{{\sqrt x  + 2}}dx} \).

Tính các tích phân sau:

a) \(\int\limits_1^3 {{e^{x - 2}}dx} \);

b) \(\int\limits_0^1 {{{\left( {{2^x} - 1} \right)}^2}dx} \);

c) \(\int\limits_0^1 {\frac{{{e^{2x}} - 1}}{{{e^x} + 1}}dx} \).

Tính các tích phân sau:

a) \(\int\limits_0^\pi  {\left( {2\cos x + 1} \right)dx} \);

b) \(\int\limits_0^\pi  {\left( {1 + \cot x} \right)\sin xdx} \);

c) \(\int\limits_0^{\frac{\pi }{4}} {{{\tan }^2}xdx} \).

Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{{\sqrt x  - 1}}{x},x > 0\). Tính giá trị của \(f\left( 4 \right) - f\left( 1 \right)\).

Tìm đạo hàm của hàm số \(F\left( x \right) = \sqrt {4x + 1} \). Từ đó, tính tích phân \(\int\limits_0^1 {\frac{1}{{\sqrt {4x + 1} }}dx} \).

Tính:

a) \(\int\limits_1^2 {\frac{{{x^4} + {x^3} + {x^2} + x + 1}}{{{x^2}}}dx} \);

b) \(\int\limits_1^2 {\frac{{x{e^x} + 1}}{x}dx} \);

c) \(\int\limits_0^1 {\frac{{{8^x} + 1}}{{{2^x} + 1}}dx} \);

d) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{{1 + {{\sin }^2}x}}{{1 - {{\cos }^2}x}}dx} \).

Tính

a) \(\int\limits_1^3 {{x^3}dx;} \)

b) \(\int\limits_0^\pi  {\cos udu.} \)

a) Cho hàm số \(f(x)\) liên tục trên đoạn \([ - 1;5]\) và \[\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = 12\]. Tính \(\int_{ - 1}^5 f (x)dx\).

b) Cho \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^3} + 2}&{{\rm{khi }}x >  - 1}\\{2x + 3}&{{\rm{khi }}x \le  - 1}\end{array}} \right.\). Tính \(\int_{ - 2}^1 f (x)dx\).