Giải các phương trình sau:
a) 2x−5=0;
b) \(4 - \frac{2}{5}x = 0\)
Sử dụng cách giải phương trình bậc nhất \({\rm{ax}} + b = 0\left( {a \ne 0} \right)\) như sau:
\(\begin{array}{l}{\rm{ax}} + b = 0\\{\rm{ax = - b}}\\x = - \frac{b}{a}\end{array}\)
Phương trình luôn có nghiệm duy nhất: \(x = - \frac{b}{a}\)
a) 2x−5=0
=> 2x=5
\( \Rightarrow x = \frac{5}{2}\)
Vậy nghiệm của phương trình là \(x = \frac{5}{2}\)
b) \(4 - \frac{2}{5}x = 0\)
=> -\(\frac{2}{5}\) x=−4
=> \(\frac{2}{5}\)x=4
=>x=4: \(\frac{2}{5}\)
=> x=10
Vậy nghiệm của phương trình là x=10
Các bài tập cùng chuyên đề
Những phương trình nào sau đây là phương trình bậc nhất một ẩn:
a) \(2{\rm{x}} + 1 = 0\)
b) \( - x + 1 = 0\)
c) \(0.x + 2 = 0\)
d) \(\left( { - 2} \right).x = 0\)
Xét phương trình bậc nhất một ẩn 2x − 6 = 0 (2)
Hãy thực hiện các yêu cầu sau để giải phương trình (2) (tức là tìm nghiệm của phương trình đó):
a) Sử dụng quy tắc chuyển vế, hãy chuyển hạng tử tự do -6 sang vế phải
b) Sử dụng quy tắc nhân, nhân cả hai vế của phương trình với \(\frac{1}{2}\) để tìm nghiệm x
Bác An gửi tiết kiệm 150 triệu đồng với kì hạn 12 tháng. Đến cuối kì (tức là sau 1 năm), bác An thu được số tiền cả vốn lẫn lãi là 159 triệu đồng. Tính lãi suất gửi tiết kiệm của bác An.
Hai bạn Vuông và Tròn giải phương trính: \(2{\rm{x}} + 5 = 16\) như sau:
Vuông: \(\begin{array}{l}2{\rm{x}} + 5 = 16\\2{\rm{x}} = 16 - 5\\2{\rm{x}} = 11\\x = \frac{{11}}{2}\end{array}\)
Tròn: \(\begin{array}{l}2{\rm{x}} + 5 = 16\\\frac{{2{\rm{x}}}}{2} + 5 = \frac{{16}}{2}\\x + 5 = 8\\x = 8 - 5\\x = 3\end{array}\)
Theo em, bạn nào đúng, bạn nào sai? Giải thích?
Hãy chỉ ra các phương trình bậc nhất một ẩn trong các phương trình sau:
a) x+1=0
b) 0x−2=0
c) 2−x=0
d) 3x=0
Giải các phương trình sau
a) 5x−4=0
b) 3+2x=0
c) 7−5x=0
d) \(\frac{3}{2}\) + \(\frac{5}{3}\)x=0
Phương trình nào sau đây là phương trình bậc nhất một ẩn
A. 0x+2=0
B. 2x+1=2x+2
C.\(2{{\rm{x}}^2}\)+1=0
D. 3x−1=0
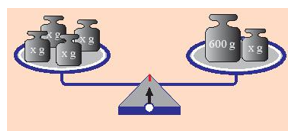
Quan sát hình bên. Biết rằng cân thăng bằng, có thể tìm được khối lượng của quả cân
không? Tìm bằng cách nào?
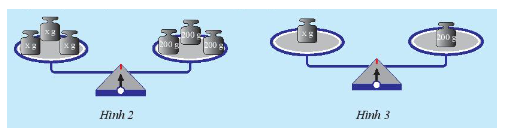
Xét cân thăng bằng ở khởi động
a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân \(x\) gam thì cân vẫn thăng bằng.
b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao?
c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
Giải các phương trình sau:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\);
b) \(2\dfrac{1}{2} - 0,75x = 0\).
Hai bạn An và Mai giải phương trình \(x = 2x\) như sau:
An: \(x = 2x\)
\(1 = 2\) (chia cả hai vế cho \(x\))
Vậy phương trình vô nghiệm.
Mai: \(x = 2x\)
\(x - 2x = 0\) (chuyển \(2x\) sang vế trái)
\( - x = 0\) (rút gọn)
\(x = 0\) (nhân hai vế với –1)
Vậy phương trình đã cho có nghiệm \(x = 0\).
Em hãy cho biết bạn nào giải đúng.
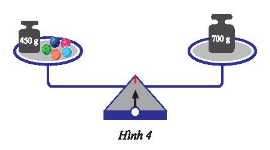
Trong Hình 4, cho biết các viên bi có cùng khối lượng là \(x\left( g \right)\) và cân bằng. Viết phương trình biểu diễn liên hệ giữa khối lượng của các vật ở hai đĩa cân.
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số \(a\) và \(b\) của phương trình bậc nhất một ẩn đó.
a) \(7x + \dfrac{4}{7} = 0\);
b) \(\dfrac{3}{2}y - 5 = 4\);
c) \(0t + 6 = 0\);
d) \({x^2} + 3 = 0\).
Đặt lên hai đĩa cân những quả cân như Hình 1.
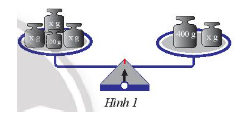
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.
b) Nếu \(x = 100\) cân có thăng bằng không? Vì sao?
Nếu \(x = 150\) thì cân có thăng bằng không? Vì sao?
Từ đó, chỉ ra một nghiệm của phương trình ở câu a.
Phương trình \(ax + b = 0\) là phương trình bậc nhất một ẩn nếu
A. \(a = 0\).
B. \(b \ne 0\).
C. \(b = 0\).
D. \(a \ne 0\).
Phương trình nào dưới đây là phương trình bậc nhất một ẩn?
A. \(3x + 2y - 6 = 0\).
B. \(3x + 6 = 0\).
C. \({x^2} = 4\).
D. \({y^2} - x + 1 = 0\).
Cho biết \(3x - 9 = 0\). Khi đó giá trị của biểu thức \({x^2} - 2x - 3\) là
A. \( - 3\).
B \(1\).
C. \(0\).
D. \(6\).
Giải phương trình: \(5x - 12 = 3\);
Giải phương trình: \(2,5y + 6 = - 6,5\);
Giải phương trình: \(\dfrac{1}{5}x - 2 = \dfrac{3}{5}\);
Quan sát phương trình (ẩn \(x\)): \(4x + 12 = 0\), nêu nhận xét về bậc của đa thức ở vế trái của phương trình đó.
Nêu hai ví dụ về phương trình bậc nhất ẩn \(x\)
Kiểm tra xem \(x = - 3\) có là nghiệm của phương trình bậc nhất \(5x + 15 = 0\) hay không.
Nêu quy tắc chuyển vế trong một đẳng thức số.
Xét đẳng thức số: \(2 + 3 - 4 = 9 - 10 + 2\). Tính giá trị mỗi vế của đẳng thức đó khi nhân cả hai vế với 5 và so sánh hai giá trị nhận được.
Giải các phương trình:
a) \( - 6x - 15 = 0\);
b) \( - \frac{9}{2}x + 21 = 0.\)
Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.
a) \(3x + 9 = 0\) với \(x = 3;\,\,x = - 3\).
b) \(2 - 2x = 3x + 1\) với \(x = - \frac{1}{5};\,\,x = \frac{1}{5}\).
Trong phòng thí nghiệm, chị Loan sử dụng cân Roberval để cân: bên đĩa thứ nhất đặt một quả cân nặng 500 g; bên đĩa thứ hai đặt hai vật cùng cân nặng \(x\) g và ba quả cân nhỏ, mỗi quả cân đó nặng 50 g. Chị Loan thấy cân thăng bằng. Viết phương trình biểu thị sự thăng bằng của cân khi đó.
Hình 4 mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1 ft = 0,3048 m). Tốc độ \(v\) (ft/s) của nước tại thời điểm \(t\) (s) được cho bởi công thức \(v = 48 - 32t\). Tìm thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa.
Giải các phương trình:
a) \(7x + 21 = 0\);
b) \( - 5x + 35 = 0\);
c) \( - \frac{1}{4}x - 1 = 0\).
