Chứng minh rằng:
a) Phương trình \({x^3} + 5{x^2} - 8{\rm{x}} + 4 = 0\) có duy nhất một nghiệm.
b) Phương trình \( - {x^3} + 3{x^2} + 24x - 1 = 0\) có ba nghiệm phân biệt.
Xét hàm số \(y = f\left( x \right)\), lập bảng biến thiên, xem xét giao điểm của đồ thị hàm số với đường thẳng \(y = 0\) và kết luận.
a) Đặt \(y = {x^3} + 5{x^2} - 8{\rm{x}} + 4\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} + 10x - 8;y' = 0 \Leftrightarrow x = - 4\) hoặc \({\rm{x}} = \frac{2}{3}\).
Bảng biến thiên:
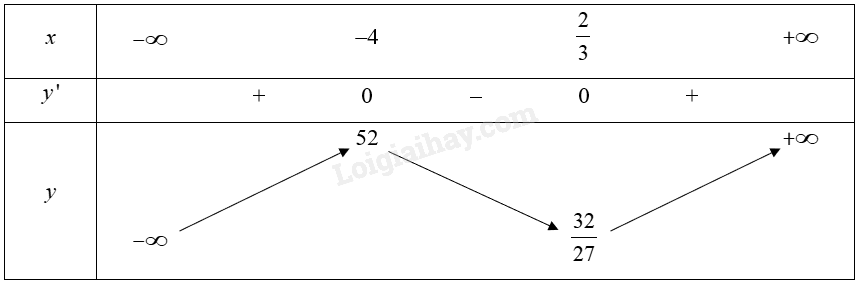
Từ bảng biển thiên, ta thấy đường thẳng \(y = 0\) giao với đồ thị của hàm số tại đúng một điểm trong khoảng \(\left( { - \infty ; - 4} \right)\). Do đó phương trình \({x^3} + 5{x^2} - 8{\rm{x}} + 4 = 0\) có duy nhất một nghiệm.
b) Đặt \(y = - {x^3} + 3{x^2} + 24x - 1\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = - 3{x^2} + 6x + 24;y' = 0 \Leftrightarrow x = 4\) hoặc \({\rm{x}} = - 2\).
Bảng biến thiên:
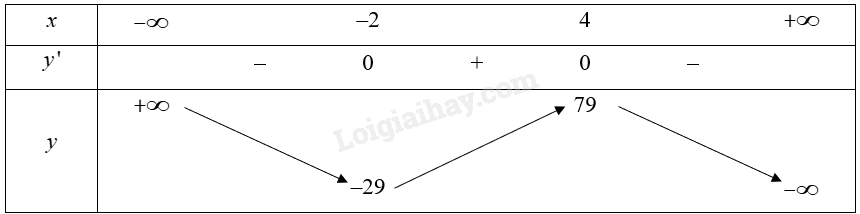
Từ bảng biển thiên, ta thấy đường thẳng \(y = 0\) giao với đồ thị của hàm số tại ba điểm phân biệt. Do đó phương trình \( - {x^3} + 3{x^2} + 24x - 1 = 0\) có ba nghiệm phân biệt.
Các bài tập cùng chuyên đề
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Cho hàm số \(y = 3{x^4} + 2\left( {m - 2018} \right){x^2} + 2017\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng \({120^0}\).
Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác có một góc ${120^o}$ là:
Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
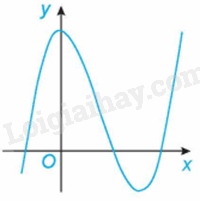
A. \(y = - {x^3} + 3{x^2} + 1\).
B. \(y = {x^3} - 3{x^2} + 3\).
C. \(y = - {x^2} + 2x + 1\).
D. \(y = \frac{{x + 1}}{{x - 1}}\).
Cho hai hàm số \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
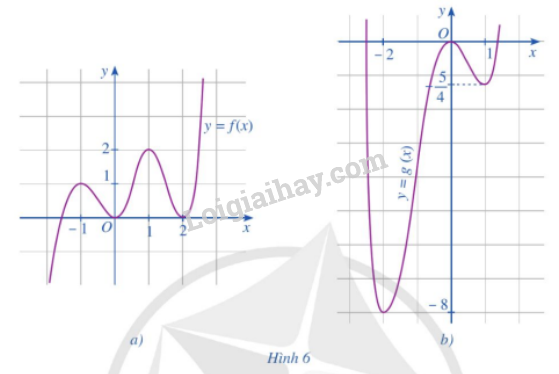
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:
a) \(y = 4{x^3} + 3{x^2}--36x + 6\)
b) \(y = \frac{{{x^2} - 2x - 7}}{{x - 4}}\)
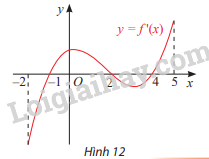
Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:
Ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({120^o}\) và có độ lớn lần lượt là 25 N và 12 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 4 N. Tính độ lớn (đơn vị: N) của hợp lực của ba lực trên (làm tròn kết quả đến hàng đơn vị).
Giá trị của tham số m để đồ thị hàm số \(y = {x^3} - 3{x^2} + m\) có hai điểm cực trị A, B thỏa mãn OA = OB (O là gốc tọa độ) có dạng \(\frac{a}{b}\) là một phân số tối giản. Tính a + b.
Hình bên là đồ thị của hàm số f’(x). Hỏi hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
Giả sử một công ty du lịch bán tour với giá là x /khách thì doanh thu sẽ được biểu diễn qua hàm số \(f(x) = - 200{x^2} + 550x\). Công ty phải bán giá tour cho một khách là bao nhiêu (đơn vị: triệu đồng) để doanh thu từ tua xuyên Việt là lớn nhất (kết quả làm tròn đến hàng phần trăm)?
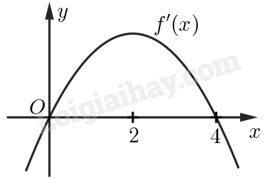
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau:
a) \(y = {x^3} - 9{x^2} - 48x + 52\);
b) \(y = - {x^3} + 6{x^2} + 9\).
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = x + \frac{1}{x}\);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = {x^2}\ln x\).
Chứng minh rằng hàm số \(f\left( x \right) = \sqrt[3]{{{x^2}}}\) không có đạo hàm tại \(x = 0\) nhưng có cực tiểu tại điểm \(x = 0\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = - x\left( {2x - 5} \right),\forall x \in \mathbb{R}\). Khẳng định nào dưới đây đúng?
A. \(f\left( { - 2} \right) < f\left( { - 1} \right)\).
B. \(f\left( 0 \right) > f\left( 2 \right)\).
C. \(f\left( 3 \right) > f\left( 5 \right)\).
D. \(f\left( 3 \right) > f\left( 2 \right)\).
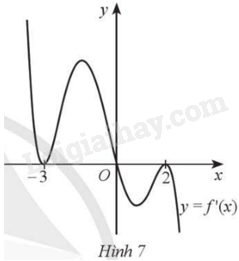
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 7. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là:
A. 4.
B. 3.
C. 2.
D. 1.
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {2^{{x^2} - 1}}\).
a) \(y' = \left( {{x^2} - 1} \right){.2^{{x^2} - 2}}\).
b) \(y' = 0\) khi \(x = - 1,x = 1\).
c) \(y\left( { - 2} \right) = 8,y\left( { - 1} \right) = 1,y\left( 1 \right) = 1\).
d) Trên đoạn \(\left[ { - 2;1} \right]\), hàm số đạt giá trị nhỏ nhất bằng 1, giá trị lớn nhất bằng 8.
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {x^3} - 3{\rm{x}} + 2\).
a) \(y' = 3{{\rm{x}}^2} - 3\).
b) \(y' = 0\) khi \(x = - 1,x = 1\).
c) \(y' > 0\) khi \(x \in \left( { - 1;1} \right)\) và \(y' < 0\) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
d) Giá trị cực đại của hàm số là ${{f}_{C}}=0$.
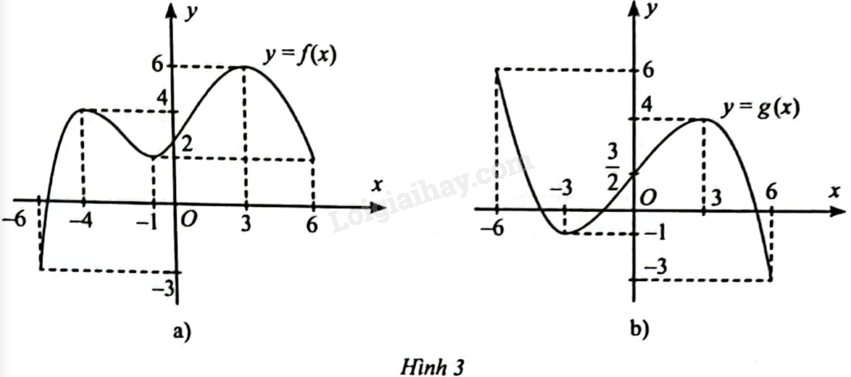
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
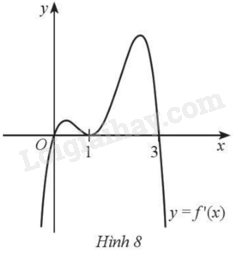
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 8.
a) \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\).
b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
c) \(f'\left( x \right) > 0\) khi \(x \in \left( {0;3} \right)\).
d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\).
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = - {x^3} - 3{x^2} + 24x - 1\);
b) \(y = {x^3} - 8{x^2} + 5x + 2\);
c) \(y = {x^3} + 2{x^2} + 3x + 1\);
d) \(y = - 3{x^3} + 3{x^2} - x + 2\).
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{3{\rm{x}} + 1}}{{{\rm{x}} - 2}}\);
b) \(y = \frac{{2{\rm{x}} - 5}}{{3{\rm{x}} + 1}}\);
c) \(y = \sqrt {4 - {x^2}} \);
d) \(y = x - \ln {\rm{x}}\).
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{{x^2} + 8}}{{x + 1}}\);
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\);
c) \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\);
d) \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}\).
Đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số \(y = f\left( x \right)\).
Chứng minh rằng
a) \(\tan x > x\) với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\);
b) \(\ln x \le x - 1\) với mọi \(x > 0\).
Tìm \(m\) để phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt.
