Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho \(\widehat {MAP} = 60^\circ \) (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.
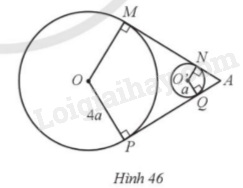
Độ dài dây curoa = độ dài cung lớn MP + độ dài cung nhỏ NQ + MN + PQ
Bước 1: Áp dụng lý thuyết về tổng 4 góc trong tứ giác để tính số đo góc MOP và góc NO’Q, từ đó suy ra số đo cung lớn MP và cung nhỏ NQ.
Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\) để tính độ dài 2 cung trên.
Bước 3: Chứng minh \(MN = PQ\), tính \(MN = AM - AN = OM.\cot \widehat {OAM} - O'N.\cot \widehat {OAM}\).
Do AM, AP là tiếp tuyến của (O) nên \(MA = PA\) và \(OM \bot MA,OP \bot PA\), do đó \(\widehat M = \widehat P = 90^\circ \) và AO là tia phân giác của góc MAP nên \(\widehat {MAO} = \widehat {PAO} = \frac{{\widehat {MAP}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Do AN, AQ là tiếp tuyến của (O’) nên \(NA = QA\) và \(O'N \bot NA,O'Q \bot QA\), do đó \(\widehat {O'NA} = \widehat {O'QA} = 90^\circ \) và AO’ là tia phân giác của góc NAQ nên \(\widehat {NAO'} = \widehat {QAO'} = \frac{{\widehat {NAQ}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Xét tứ giác OMAP có \(\widehat {MOP} + \widehat M + \widehat {MAP} + \widehat P = 360^\circ \) nên \(\widehat {MOP} = 360^\circ - \left( {\widehat M + \widehat {MAP} + \widehat P} \right)\)\( = 360^\circ - \left( {90^\circ + 60^\circ + 90^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ MP là 120⁰
Số đo cung lớn MP là \(360^\circ - 120^\circ = 240^\circ \) và có độ dài là \({l_1} = \frac{{\pi .4a.240}}{{180}} = \frac{{16\pi a}}{3}\)
Xét tứ giác O’NAQ có \(\widehat {NO'Q} + \widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ} = 360^\circ \) nên \(\widehat {NO'Q} = 360^\circ - \left( {\widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ}} \right)\) \( = 360^\circ - \left( {90^\circ + 90^\circ + 60^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ NQ là 120⁰ và có độ dài là \({l_2} = \frac{{\pi .a.120}}{{180}} = \frac{{2\pi a}}{3}\)
Ta có: \(MN = MA - NA;PQ = PA - QA\), mà \(MA = PA;NA = QA\) suy ra \(MN = PQ\).
Xét tam giác OAM vuông tại M có:
\(MA = OM.\cot \widehat {OAM} = a.\cot 30^\circ = 4a\sqrt 3 \).
Xét tam giác O’AN vuông tại N có:
\(NA = ON.\cot O'AN = a.\cot 30^\circ = a\sqrt 3 \).
Ta có: \(MN = PQ = MA - NA = 4a\sqrt 3 - a\sqrt 3 = 3\sqrt 3 a\)
Độ dài dây Curoa mắc qua 2 ròng rọc là:
\(\frac{{16\pi a}}{3} + \frac{{2\pi a}}{3} + 3\sqrt 3 a + 3\sqrt 3 a = 6a\left( {\pi + \sqrt 3 } \right)\).
Các bài tập cùng chuyên đề
Chu vi đường tròn bán kính \(R = 9\) là
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
Tính độ dài cung \(30^\circ \) của một đường tròn có bán kính \(4\,dm\)
Số đo \(n^\circ \) của cung tròn có độ dài \(30,8\,cm\) trên đường tròn có bán kính \(22\,cm\) là ( lấy \(\pi \approx 3,14\) và làm tròn đến độ)
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng?
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là
Chu vi đường tròn bán kính \(R = 6\) là
Tính độ dài cung \(45^\circ \) của một đường tròn có bán kính \(5\,dm\)
Số đo \(n^\circ \) của cung tròn có độ dài \(40,2\,cm\) trên đường tròn có bán kính \(16\,cm\) là (lấy \(\pi \approx 3,14\) và làm tròn đến độ)
Cho ba điểm $A,B,C$ thẳng hàng sao cho $C$ nằm giữa $A$ và $B$, đồng thời \(AB = 3AC.\) Khẳng định nào sau đây sai?
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây \(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(6\pi \,(cm).\) Độ dài cung lớn \(BC\) là
Biết rằng trên một đường tròn, hai cung bằng nhau thì có cùng độ dài và độ dài của cung tỉ lệ với số đo của nó. Từ đó hay lập công thức tính độ dài cung \(n^\circ \) của đường tròn bán kính R bằng cách thực hiện các bước sau:
a) Từ (1), tính độ dài của cung \(1^\circ .\)
b) Tính độ dài \(l\) của cung \(n^\circ .\)
Tính độ dài cung \(40^\circ \) của đường tròn bán kinh 9 cm.
Bánh xe (khi bơm căng) của một chiếc xe đạp có đường kính 650 mm. Biết rằng khi giò đĩa quay một vòng thì bánh xe đạp quay được khoảng 3,3 vòng (H.5.14). Hỏi chiếc xe đạp di chuyển được quãng đường dài bao nhiêu mét sau khi người đi xe đạp 10 vòng liên tục?
Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng \(70^\circ .\)
a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau.
b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười).
Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa (bánh răng gắn với bàn đạp), một chiếc líp (cũng có dạng bánh răng) gắn với bánh xe và bộ xích (H.5.23). Biết rằng giò đĩa có bán kính 15 cm, líp có bán kính 4 cm và bánh xe có đường kính 65 cm. Hỏi khi người đi xe đạp một vòng thì xe chạy được quãng đường dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
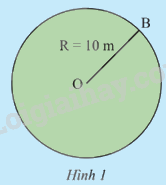
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:
a) Độ dài của toàn bộ hàng rào
b) Độ dài của mỗi phần hàng rào
c) Độ dài của n phần hàng rào.
Tính độ dài cung 72o của một đường tròn bán kính 25 cm.
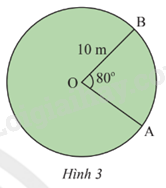
Tính độ dài của của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết \(\widehat {AOB} = {80^o}\).
Tính độ dài các cung \({30^o};{90^o};{120^o}\) của đường tròn (O; 6 cm)
Lấy một vòng tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b. Đo chiều dài sợi dây đó.
Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười).
a) Đánh dấu hai điểm \(A,B\) trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung \(AB\) của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b. Đo chiều dài sợi dây đó.
b) Ta coi mỗi đường tròn bán kính \(R\) là một cung tròn có số đo \(360^\circ \). Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng \(1^\circ \); chu vi của đường tròn khi đó cũng được chia thành \(360\) phần bằng nhau. Tính theo \(R\):
+ Độ dài cung tròn có số đo \(1^\circ \);
+ Độ dài cung tròn có số đo \(n^\circ \).
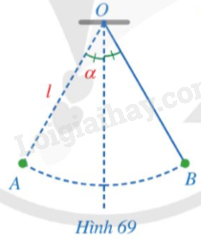
Một con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\) (Hình 69). Tính độ dài quãng đường \(AB\) mà con lắc đó di chuyển, biết rằng sợi dây \(OA\) có độ dài bằng \(l\) và tia \(OA\) tạo với phương thẳng đứng góc \(\alpha \).
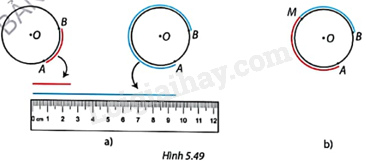
Cắt một hình tròn bằng giấy và đánh dấu hai điểm A, B bất kì trên mép của hình tròn.
a) Sử dụng dây mềm để lần lượt viền theo hai cung AB như Hình 5.49a và đo độ dài của đoạn dây trong mỗi trường hợp.
b) Lấy một điểm M bất kì trên cung AB, chia cung AB thành hai cung AM và MB. So sánh tổng độ dài hai đoạn dây được viền theo cung AB và MB với độ dài đoạn dây được viền theo cung AB (Hình 5.49b).
Tính độ dài cung \({235^o}\) của đường tròn bán kính 7cm.
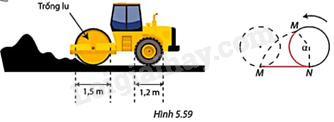
Một chiếc xe lu có đường kính trống lu là 1,5m và đường kính của bánh sau là 1,2m (Hình 5.59). Khi hoạt động, trống lu quay hết một vòng \(\left( {{{360}^o}} \right)\) trong 5 phút.
a) Trong mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường?
b) Để cán được 1 mét đường thì trống lu phải quay một góc bao nhiêu độ?
c) Để trống lu quay được 1 vòng thì bánh sau phải quay bao nhiêu vòng?
Độ dài cung \({30^o}\) của đường tròn bán kính 6cm là
A. \(\frac{\pi }{2}\)cm.
B. \(\pi \)cm.
C. 2\(\pi \)cm.
D. 3\(\pi \)cm.
Vĩ độ của Hà Nội là \(20^\circ 01'\), mỗi vòng kinh tuyến dài khoảng 40000km. Tính độ dài cung kinh tuyến từ Hà Nội đến xích đạo.
