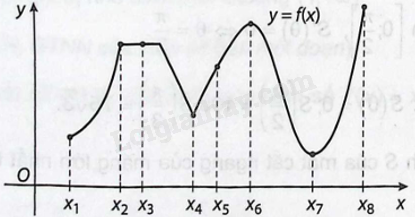
Sử dụng đồ thị dưới đây, xác định xem hàm số \(y = f\left( x \right)\) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}\) hay không.
Quan sát đồ thị kết hợp với định nghĩa cực trị, giá trị lớn nhất, nhỏ nhất của hàm số để đưa ra kết luận.
Ta có hàm số \(y = f\left( x \right)\) xác định trên \(\left[ {{x_1};{x_8}} \right]\). Từ đồ thị ta có:
+ \(f\left( x \right) \le f\left( {{x_8}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_8} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_8}} \right)\). Do đó hàm số đạt giá trị lớn nhất tại điểm \({x_8}\).
+ \(f\left( x \right) \ge f\left( {{x_7}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_7} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_7}} \right)\). Do đó hàm số
đạt giá trị nhỏ nhất tại điểm \({x_7}\).
Ta có hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ {{x_1};{x_8}} \right]\).
+ Gọi \({h_1} = \frac{{{x_5} - {x_4}}}{2}\) , ta thấy \({h_1}\) dương. Vì \(f\left( x \right) > f\left( {{x_4}} \right)\) với mọi \(x \in \left( {{x_4} - {h_1};{x_4} + {h_1}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_4}\) nên hàm số đạt cực tiểu tại điểm \({x_4}\).
+ Tương tự, gọi \({h_2} = \frac{{{x_8} - {x_7}}}{2}\) , ta thấy \({h_2}\) dương. Vì \(f\left( x \right) > f\left( {{x_7}} \right)\) với mọi \(x \in \left( {{x_7} - {h_2};{x_7} + {h_2}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_7}\) nên hàm số đạt cực tiểu tại điểm \({x_7}\).
+ Gọi \({h_3} = \frac{{{x_6} - {x_5}}}{2}\) , ta thấy \({h_3}\) dương. Vì \(f\left( x \right) < f\left( {{x_6}} \right)\) với mọi \(x \in \left( {{x_6} - {h_3};{x_6} + {h_3}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_6}\) nên hàm số đạt cực đại tại điểm \({x_6}\).

Các bài tập cùng chuyên đề
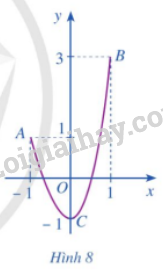
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
Nếu hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) = \sin x - 2023,\forall x \in \mathbb{R}\) thì giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng:
A. \(f\left( 0 \right)\).
B. \(f\left( 1 \right)\).
C. \(f\left( {1,5} \right)\).
D. \(f\left( 2 \right)\).
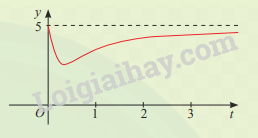
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t \( \ge \) 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
c) \(h(x) = x\sqrt {2 - {x^2}} \)
Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày.
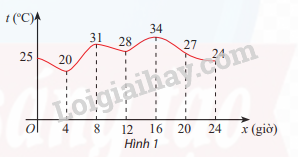
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là \(28^\circ C\).
ii) Nhiệt độ cao nhất trong ngày là \(40^\circ C\).
iii) Nhiệt độ cao nhất trong ngày là \(34^\circ C\).
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
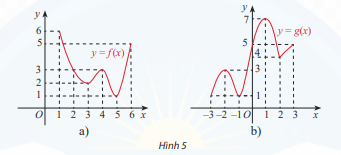
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5
Cho hàm số f(x) có đồ thị như hình dưới đây:
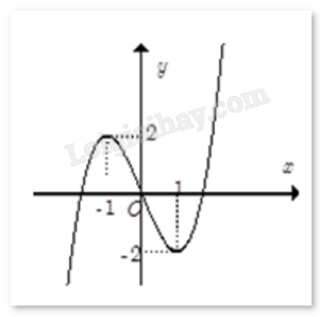
Giá trị lớn nhất của hàm số đã cho trên [-1;1] là:
-
A.
y = 2
-
B.
y = 1
-
C.
x = 2
-
D.
y = 0
Cho hàm số y = f(x) liên tục trên đoạn [−1;4] và có đồ thị như hình vẽ dưới đây.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;4]. Tính M + m.
-
A.
4
-
B.
3
-
C.
2
-
D.
1
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
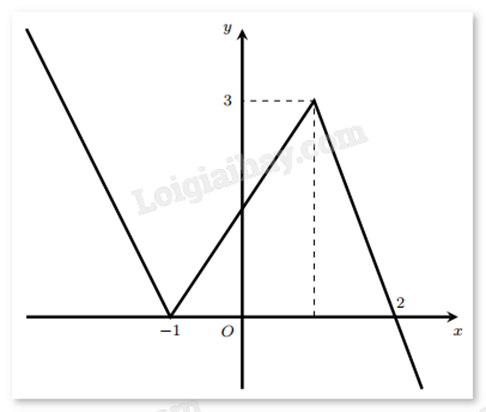
Tìm giá trị lớn nhất của hàm số g(x) = 2f(x) – 1trên đoạn [–1;2].
-
A.
3
-
B.
4
-
C.
5
-
D.
6
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
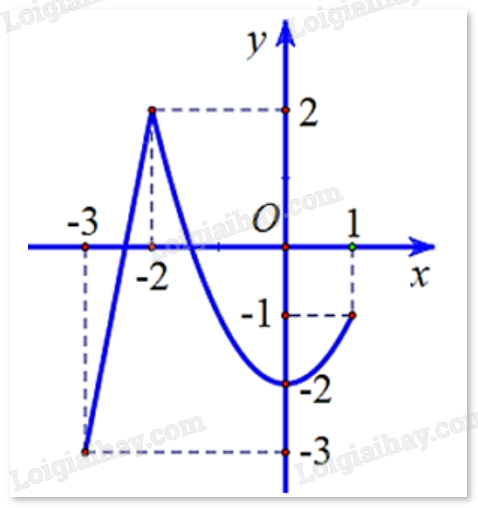
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;1]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
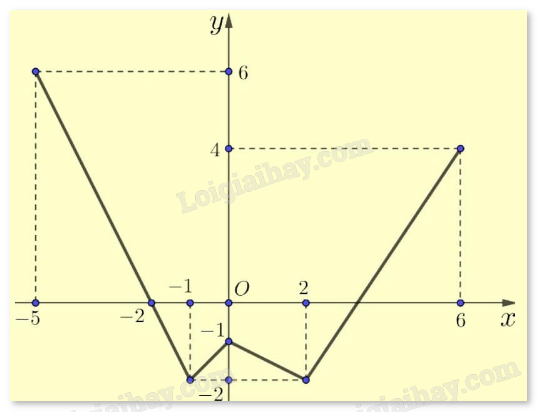
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;2]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
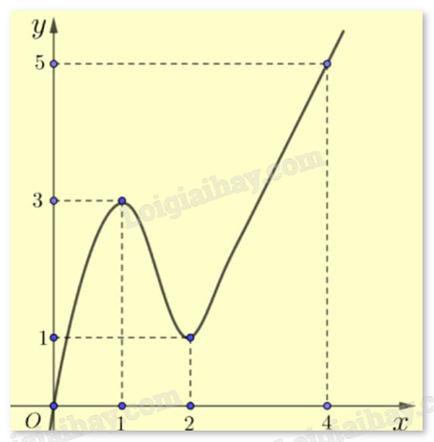
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Tính M - m.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
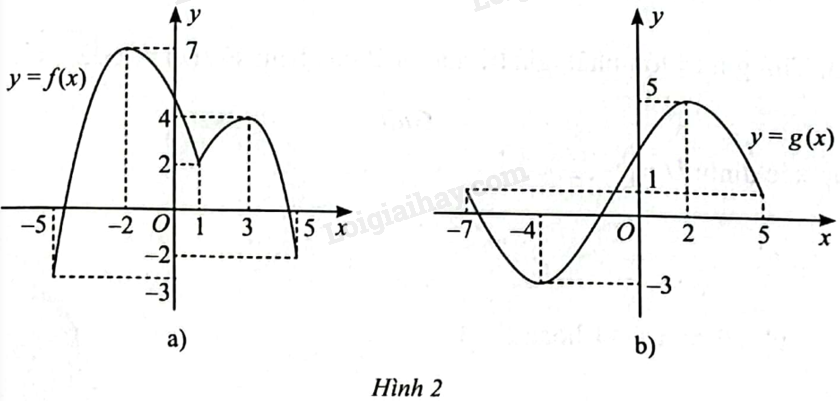
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.
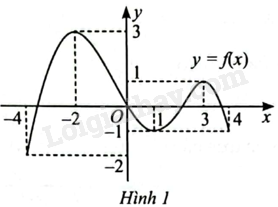
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\) trong Hình 1 là:
A. ‒1.
B. ‒2.
C. 0.
D. 1.
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y = - {x^3} + 300{x^2}\) (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.
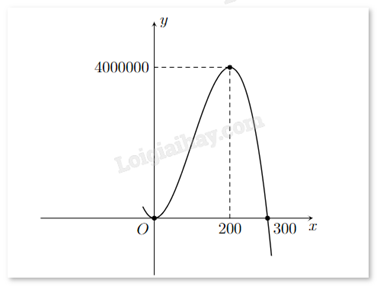
Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận dự kiến thu được nhiều nhất?
-
A.
4000000
-
B.
200
-
C.
300
-
D.
150
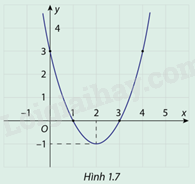
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho.
b) Khi \(x\) thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\) có giá trị lớn nhất.
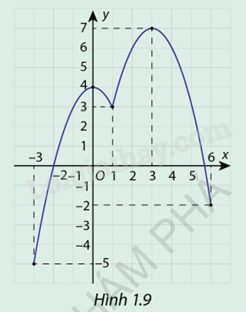
Cho hàm số \(y = f(x)\) liên tục trên đoạn, có đạo hàm trên các khoảng \(( - 3;1)\)và \((1;6)\) có dồ thị hàm số như hình 1.9, biết rằng \(f( - 3) = - 5\) và \(f(6) = - 2\).
a) Xác định các điểm cực trị thuộc đoạn \([ - 3;6]\) của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \([ - 3;6]\).
Cho hàm số \(y = {x^2}\), biết \({x^2} \ge 0,\forall x \in R\) và \({x^2} = 0 \Leftrightarrow x = 0 \Rightarrow y = 0\). Khi đó \(y = 0\) là:
-
A.
GTNN của hàm số.
-
B.
GTLN của hàm số.
-
C.
GTNN của đồ thị hàm số.
-
D.
GTLN của đồ thị hàm số.
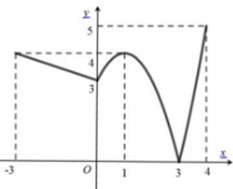
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;4} \right]\). Tính \(M + m\).
-
A.
5
-
B.
8
-
C.
7
-
D.
1
Cho hàm số f(x) có đồ thị như hình dưới.
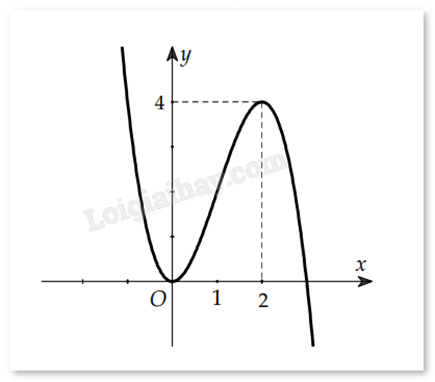
Giá trị lớn nhất của hàm số f(x) là
-
A.
1
-
B.
2
-
C.
4
-
D.
Đáp án khác
Cho hàm số f(x) có đồ thị như hình dưới.
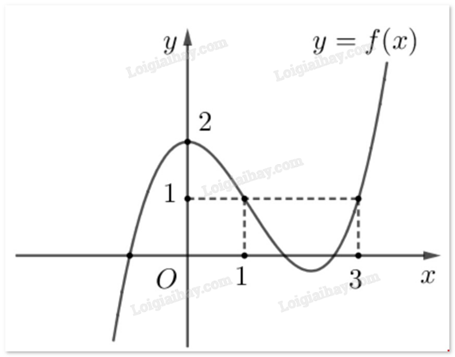
Giá trị lớn nhất của hàm số f(x) trên đoạn [0;3] là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Cho hàm số f(x) có bảng biến thiên như hình dưới.
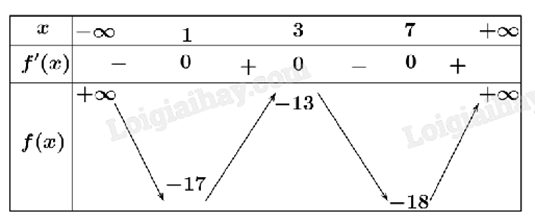
Giá trị nhỏ nhất của hàm số f(x) là
-
A.
-13
-
B.
-17
-
C.
-18
-
D.
7
Cho hàm số f(x) có đồ thị như hình dưới.
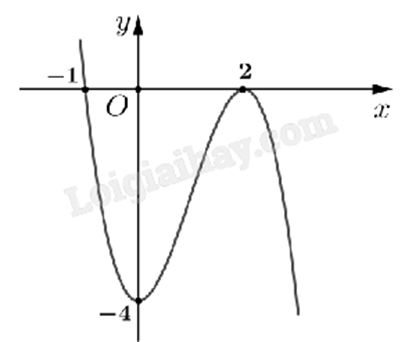
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;2] là
-
A.
-1
-
B.
-4
-
C.
2
-
D.
0
Cho hàm số f(x) có đồ thị như hình dưới.
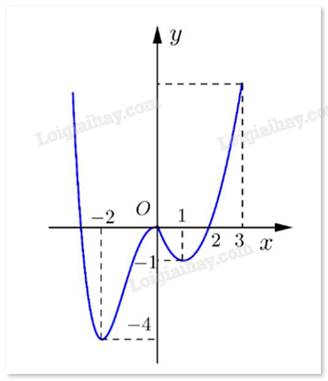
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;3] là
-
A.
-1
-
B.
1
-
C.
2
-
D.
3
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ sau:
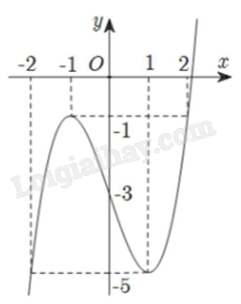
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số đã cho trên đoạn [-2;2] bằng
-
A.
0
-
B.
-1
-
C.
-5
-
D.
-6
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng
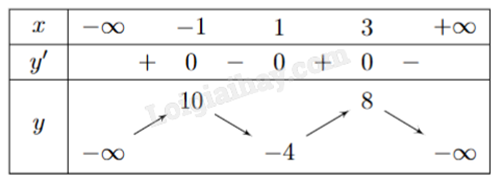
-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Cho hàm số y = f(x) có bảng biến thiên như hình. Giá trị nhỏ nhất của hàm số y = f(x) trên [-1;1] bằng
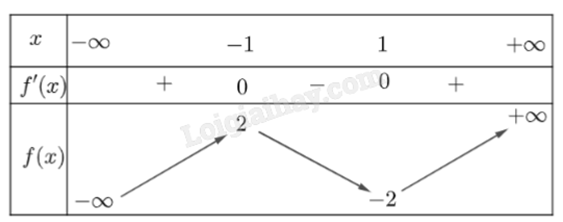
-
A.
-3
-
B.
-1
-
C.
-2
-
D.
1
Cho hàm số y = f(x) liên tục và có đồ thị trên đoạn [-2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên đoạn [-2;4] bằng
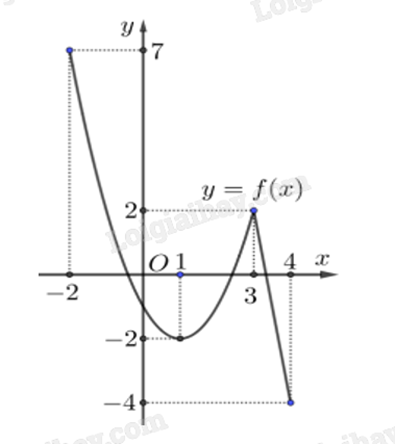
-
A.
-2
-
B.
5
-
C.
3
-
D.
0
Cho hàm số y = f(x) liên tục trên đoạn [–1;2] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;2]. Tính M + 2m.
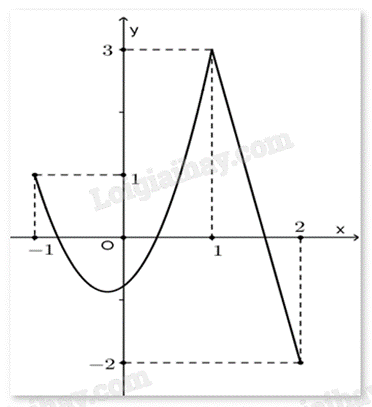
-
A.
y = 2
-
B.
y = -1
-
C.
y = 0
-
D.
y = 1
Cho hàm số f(x) có đồ thị như hình dưới đây:
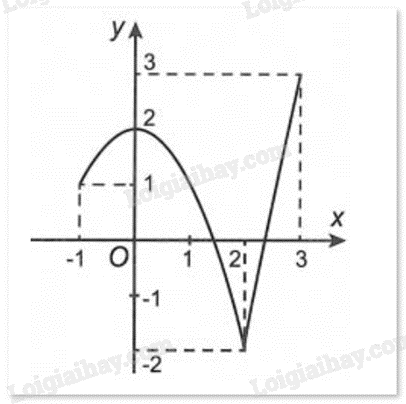
Giá trị lớn nhất của hàm số đã cho trên [-1;3] là:
-
A.
y = 1
-
B.
y = 2
-
C.
y = -2
-
D.
y = 3







Danh sách bình luận