Dãy số \(\frac{1}{2};0; - \frac{1}{2}; - 1;\frac{{ - 3}}{2};...\) là cấp số cộng với

Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} =  - 2n + 3\). Chứng minh rằng \(\left( {{u_n}} \right)\) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này.

Dãy số không đổi a, a, a, ... có phải là một cấp số cộng không?

Cho dãy số \(\left( {{u_n}} \right)\) gồm tất cả các số tự nhiên lẻ, xếp theo thứ tự tăng dần

a) Viết năm số hạng đầu của dãy số.

b) Dự đoán công thức biểu diễn số hạng \({u_n}\) theo số hạng \({u_{n - 1}}\).

Cho dãy số (un) với \({u_n} =  - 5n + 7(n \ge 1).\)Dãy (\({u_n}\)) có là cấp số cộng không? Vì sao? 

Cho (u_n) là cấp số cộng \({u_1}\; = {\rm{ }}-{\rm{ }}7,{\rm{ }}{u_2}\; = {\rm{ }}-{\rm{ }}2.\) Viết năm số hạng đầu của cấp số cộng đó.

Cho dãy số \( - 2;3;8;13;18;23;28\)

Kể từ số hạng thứ hai, nêu mối liên hệ của mỗi số hạng với số hạng đứng ngay trước nó.

Trong các dãy số sau, dãy số nào là cấp số cộng? Vì sao?

a)    \(10; - 2; - 14; - 26; - 38\)

b)    \(\frac{1}{2};\frac{5}{4};2;\frac{{11}}{4};\frac{7}{2}\)

c)    \(1^2; 2^2; 3^2; 4^2; 5^2 \)

d)    1; 4; 7; 10; 13

Trong các dãy số sau, dãy số nào là cấp số cộng?
A. \(21; - 3; - 27; - 51; - 75\)
B. \(\frac{1}{2};\frac{5}{4};2;\frac{{11}}{4};\frac{{15}}{4}\)
C. \(\sqrt 1 ,\sqrt 2 ,\sqrt 3 ,\sqrt 4 ,\sqrt 5 \)
D. \(\frac{1}{{20}};\frac{1}{{30}};\frac{1}{{40}};\frac{1}{{50}};\frac{1}{{60}}\)

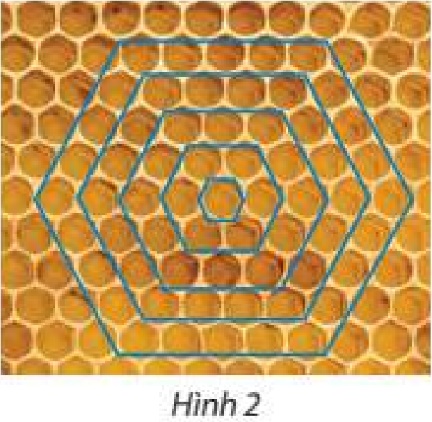
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.

Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.

a) 3; 7; 11; 15; 19; 23.

b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).

c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.

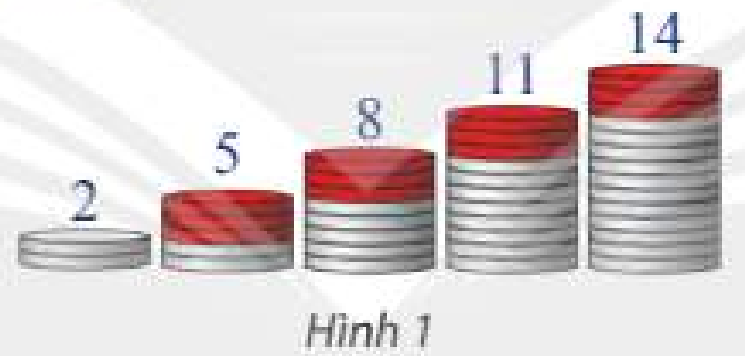
Tìm điểm giống nhau của các dãy số sau:

a) 2; 5; 8; 11; 14 (xem Hình 1). 

b) 2; 4; 6; 8.                     

c) 5; 10; 15; 20; 25.          

d) ‒5; ‒2; 1; 4; 7; 10.

Chứng minh dãy số hữu hạn sau là cấp số cộng: \(1; - 3; - 7; - 11; - 15\).

Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.

a) \({u_n} = 3 - 4n\);      

b) \({u_n} = \frac{n}{2} - 4\);                             

c) \({u_n} = {5^n}\); d) \({u_n} = \frac{{9 - 5n}}{3}\).

Dãy số nào sau đây là cấp số cộng?

Dãy số nào sau đây là cấp số cộng?

Dãy số nào sau đây là cấp số cộng?

Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} =  - 3\), \({u_7} = 21\). Khi đó công sai d là

Trong các dãy số \(\left( {{u_n}} \right)\) với số hạng tổng quát sau, dãy số nào là cấp số cộng?

A. \({u_n} = {3^n}\)                                                     

B. \({u_n} = 1 - 3n\)

C. \({u_n} = {3^n} + 1\)                                               

D. \({u_n} = 3 + {n^2}\)

Cho ba số \(\frac{1}{{b + c}}\), \(\frac{1}{{c + a}}\), \(\frac{1}{{a + b}}\) theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số \({a^2}\), \({b^2}\), \({c^2}\) theo thứ tự cũng lập thành một cấp số cộng.

Chọn cấp số cộng trong các dãy số (\({u_n}\)) sau

A.\({u_n} = {3^n} + 2\)                             

B.\({u_n} = \frac{3}{n} + 1\)           

C. \({u_n} = 3n\)                                       

D.\({u_1} = 1,\,\,{u_{n + 1}} = {u_n} + n\).

Trong các dãy số \(\left( {{u_n}} \right)\) cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.

a) \({u_n} = 2n + 3\);

b) \({u_n} =  - 3n + 1\);

c) \({u_n} = {n^2} + 1\);

d) \({u_n} = \frac{2}{n}\).

Trong các dãy số \(\left( {{u_n}} \right)\) cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.

a) \({u_n} = 3n + 1\);

b) \({u_n} = 4 - 5n\);

c) \({u_n} = \frac{{2n + 3}}{5}\);

d) \({u_n} = \frac{{n + 1}}{n}\);

e) \({u_n} = \frac{n}{{{2^n}}}\);

g) \({u_n} = {n^2} + 1\).