Tìm số đo các góc B và C của tam giác ABC trong Hình 4.6.
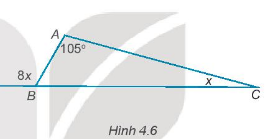
Áp dụng tổng 3 góc trong 1 tam giác bằng 180 độ.
Ta có: \(8x+\widehat{B} = 180^0\) (2 góc kề bù) nên \(\widehat{B} = 180^0-8x\)
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = {180^0}\) (Định lí tổng 3 góc trong 1 tam giác)
\(\begin{array}{l} {105^0} + \left( {{{180}^0} - 8x} \right) + x = {180^0}\\ - 7x = {180^0} - {105^0} - {180^0}\\ - 7x = - {105^0}\\ x = {15^0}\end{array}\)
Do đó, \(\widehat{C} = x = 15^0\)
\(\widehat{B} = 180^0-8x=180 - 8.15=60^0\)

Các bài tập cùng chuyên đề
Góc ngoài của tam giác là:
-
A.
góc kề bù với một góc trong của tam giác
-
B.
góc phụ nhau với một góc trong của tam giác
-
C.
bằng hiệu của hai góc trong không kề với nó
-
D.
bằng góc kề với nó
Tìm số đo góc x trong Hình 4.7.
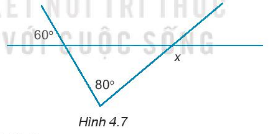
Tìm các số đo góc x, y trong Hình 4.5.
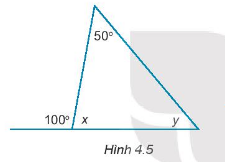
Quan sát hình 3:
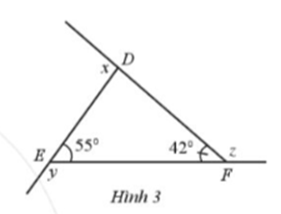
a) Tính số đo góc x, y, z.
b) Hãy nhận xét về tổng các số đo góc x + y + z
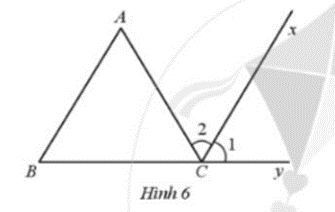
Ở Hình 6 có \(\hat A = \hat B = 60^\circ \) và Cx là tia phân giác của góc ACy. Chứng minh Cx song song với AB.
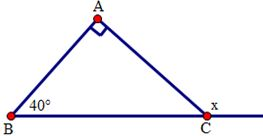
Cho hình sau. Tính số đo x:
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)







Danh sách bình luận