Biết rằng nhiệt lượng tỏa ra trên dây dẫn được tính bởi công thức \(Q = {I^2}Rt\), trong đó Q là nhiệt lượng tính bằng đơn vị Joule (J), R là điện trở tính bằng đơn vị Ohm \(\left( \Omega \right)\), I là cường độ dòng điện tính bằng đơn vị Ampe (A), t là thời gian tính bằng giây (s).
Dòng điện chạy qua một dây dẫn có \(R = 10\Omega \) trong thời gian 5 giây.
a) Thay dấu “?” trong bảng bằng các giá trị thích hợp.

b) Cường độ dòng điện phải là bao nhiêu Ampe để nhiệt lượng tỏa ra trên dây dẫn đạt 800J?
a) + Thay \(R = 10\Omega \) và \(t = 5\) (giây) vào biểu thức \(Q = {I^2}Rt\) ta có \(Q = 50{I^2}\).
+ Thay lần lượt các giá trị của I vào công thức \(Q = 50{I^2}\) ta tính được các giá trị Q tương ứng.
b) Thay \(Q = 800\left( J \right)\) vào công thức \(Q = 50{I^2}\), ta tính được I.
a) Theo giả thiết \(R = 10\left( \Omega \right)\) và \(t = 5\) (giây) nên \(Q = 50{I^2}\).
Tính giá trị của biểu thức \(Q = 50{I^2}\) lần lượt tại \(I = 1;I = 1,5;I = 2\) ta được bảng

b) Nếu \(Q = 800\left( J \right)\) thì \(800 = 50{I^2}\) hay \({I^2} = 16\) và \(I = 4\). Vậy để nhiệt lượng tỏa ra trên dây dẫn đạt 800J, cường độ dòng điện phải là 4 Ampe.

Các bài tập cùng chuyên đề
Tìm các số $x$ không âm thỏa mãn $\sqrt x \ge 3$
-
A.
$x \ge 9$
-
B.
$x < 9$
-
C.
$x > 9$
-
D.
$x \le 9$
Cho biểu thức \(C = \sqrt {2x - 1} .\)
a) Tính giá trị của biểu thức tại \(x = 5.\)
b) Tại \(x = 0\) có tính được giá trị của biểu thức không? Vì sao?
Cho căn thức \(\sqrt {5 - 2x} .\)
a) Tìm điều kiện xác định của căn thức.
b) Tính giá trị của căn thức tại \(x = 2.\)
Trở lại tình huống mở đầu.
Tình huống mở đầu
Trong Vật lí, quãng đường S (tính bằng mét) của một vật tự rơi tự do được cho bởi công thức \(S = 4,9{t^2},\) trong đó t là thời gian rơi (tính bằng giây) . Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?
a) Viết công thức tính thời gian t (giây) cần thiết để vật rơi được quãng đường S (mét)
b) Sử dụng công thức tìm được trong câu a, hãy trả lời câu hỏi trong tình huống mở đầu
Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng \(2\,{m^2}.\) Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét?
Tìm điều kiện xác định của \(\sqrt {x + 10} \) và tính giá trị của căn thức tại \(x = - 1.\)
Kích thước màn hình ti vi hình chữ nhật được xác định bởi độ dài đường chéo. Một loại ti vi có tỉ lệ hai cạnh màn hình là 4:3.
a) Gọi x (inch) là chiều rộng của màn hình tivi. Viết công thức tính độ dài đường chéo d (inch) của màn hình ti vi theo x.
b) Tính chiều rộng và chiều dài (theo centimet) của màn hình ti vi loại 40 inch.
Chứng minh rằng:
a) \({\left( {1 - \sqrt 2 } \right)^2} = 3 - 2\sqrt 2 ;\)
b) \({\left( {\sqrt 3 + \sqrt 2 } \right)^2} = 5 + 2\sqrt 6 .\)
Trong Vật lí, tốc độ (m/s) của một vật đang bay được cho bởi công thức \(v = \sqrt {\frac{{2E}}{m}} ,\) trong đó E là động năng của vật (tính bằng Joule, kí hiệu là J) và m (kg) là khối lượng của vật (Theo sách Vật lí đại cương, NXB Giáo dục Việt Nam, 2016) .
Tính tốc độ bay của một vật khi biết vật đó có khối lượng 2,5 kg và động năng 281,25 J.
Với giá trị nào của x thì biểu thức A = \(\sqrt {3x + 6} \) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai).
Cho biểu thức P = \(\sqrt {{a^2} - {b^2}} \). Tính giá trị của P khi:
a) a = 5; b = 0
b) a = 5; b = -5
c) a = 2; b = -4
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)

a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).
Tính giá trị của các biểu thức:
a) \({\left( {\sqrt {5,25} } \right)^2} + {\left( { - \sqrt {1,75} } \right)^2}\)
b) \({\left( {\sqrt {102} } \right)^2} - \sqrt {{{98}^2}} \)
Tính giá trị của các biểu thức sau khi x = 16; y = 9
a) \(\sqrt x + \sqrt y \)
b) \(\sqrt {x + y} \)
c) \(\frac{1}{2}\sqrt {xy} \)
d) \(\frac{1}{6}x\sqrt y \)
Cho biểu thức P = \(\sqrt {{x^2} - xy + 1} \). Tính giá trị của P khi:
a) x = 3; y = - 2
b) x = 1; y = 4
Kết quả của phép tính \(\sqrt {27} :\sqrt 6 .2\sqrt {18} \) là
A. 12
B. 18
C. 72
D. 144
Tìm các số \(x\) không âm thỏa mãn \(\sqrt {5x} < 10\)
-
A.
\(0 \le x < 20\)
-
B.
\(x < 20\)
-
C.
\(x > 0\)
-
D.
\(x < 2\)
Tìm giá trị của $x$ không âm biết $2\sqrt x - 30 = 0$.
-
A.
$x = - 15$
-
B.
$x = 225$
-
C.
$x = 25$
-
D.
$x = 15$
Khẳng định nào sau đây đúng về nghiệm ${x_0}$ của phương trình \(\dfrac{{9x - 7}}{{\sqrt {7x + 5} }} = \sqrt {7x + 5} \)
-
A.
${x_0} < 5$
-
B.
${x_0} > 8$
-
C.
${x_0} > 9$
-
D.
$5 < {x_0} < 7$
Tính giá trị biểu thức \(A = \dfrac{1}{{1 + \sqrt 3 }} + \dfrac{1}{{\sqrt 3 + \sqrt 5 }} + \dfrac{1}{{\sqrt 5 + \sqrt 7 }} \)\(+ ... + \dfrac{1}{{\sqrt {2019} + \sqrt {2021} }}\)
-
A.
\(1 - \sqrt {2021} \)
-
B.
\(\sqrt {2021} - 1\)
-
C.
\(\dfrac{{\sqrt {2021} - 1}}{2}\)
-
D.
\(\dfrac{{\sqrt {2019} - 1}}{2}\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{{x + \sqrt x + 4}}{{\sqrt x }}\) với \(x > 0\)
-
A.
\(5\)
-
B.
\(9\)
-
C.
\(4\)
-
D.
\(0\)
Cho \(A = \dfrac{1}{{\sqrt 3 - 1}} - \sqrt {27} + \dfrac{3}{{\sqrt 3 }};\)\(B = \dfrac{{5 + \sqrt 5 }}{{\sqrt 5 + 2}} + \dfrac{{\sqrt 5 }}{{\sqrt 5 - 1}} - \dfrac{{3\sqrt 5 }}{{3 + \sqrt 5 }}\). Chọn câu đúng.
-
A.
\(B > A > 0\)
-
B.
\(A < B < 0\)
-
C.
\(A < 0 < B\)
-
D.
\(B < 0 < A\)
Tính giá trị của \(A =\dfrac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \dfrac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \dfrac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\)
-
A.
\(A=1-\dfrac{2}{\sqrt{2018}}\)
-
B.
\(A=1-\dfrac{1}{\sqrt{2028}}\)
-
C.
\(A=1-\dfrac{1}{\sqrt{2015}}\)
-
D.
\(A=1-\dfrac{1}{\sqrt{2018}}\)
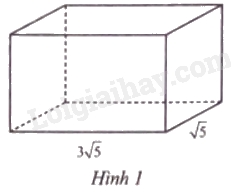
Cho hình hộp chữ nhật với chiều dài \(3\sqrt 5 \) cm, chiều rộng \(\sqrt 5 \) cm và thể tích \(30\sqrt 5 \) cm3 như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó.
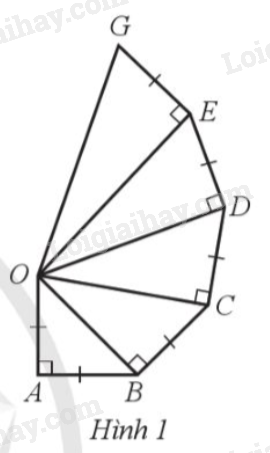
Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\)
Trên một đoạn sông, tốc độ dòng chảy của nước ở bề mặt sông lớn hơn tốc độ dòng chảy của nước ở đáy sông. Gọi v (km/h) là tốc độ dòng chảy của nước ở bề mặt sông và f (km/h) là tốc độ dòng chảy của nước ở đây sông. Khi đó, ta có công thức: \(\sqrt f = \sqrt v - 1,3\).
a) Tính tốc độ dòng chảy của nước ở đáy sông, biết tốc độ dòng chảy của nước ở bề mặt sông là 9 km/h.
b) Tính tốc độ dòng chảy của nước ở bề mặt sông, biết tốc độ dòng chảy của nước ở đáy sông là 20,25 km h.
Tính giá trị của mỗi biểu thức:
a) \(\sqrt {2x + 7} \) với \(x = 1;x = \frac{2}{3};x = 2\sqrt 3 .\)
b) \(\sqrt { - {x^2} + 2x + 11} \) với \(x = 0;x = \frac{1}{2};x = \sqrt 5 .\)
c) \(\sqrt[3]{{{x^3} + 3{x^2} + 3x + 1}}\) với \(x = - 1;x = - \frac{1}{3};x = \sqrt 2 .\)
Điện áp U (V) yêu cầu cho một mạch điện được cho bởi công thức \(U = \sqrt {P.R} \), trong đó P (W) là công suất tiêu thụ của điện trở và R (Ω) là giá trị điện trở.
a) Tính điện áp để thắp sáng cho bóng đèn A có công suất tiêu thụ là 100 W và giá trị điện trở là 110 Ω (làm tròn kết quả đến hàng đơn vị của vôn).
b) Bóng đèn B có điện áp 110 V và giá trị điện trở là 88 Ω. Công suất tiêu thụ của bóng đèn B có lớn hơn công suất tiêu thụ của bóng đèn A hay không? Vì sao?
Tốc độ v (m/s) của một chiếc ca nô được tính theo độ dài đường sóng nước sau đuôi \(l\) (m) của ca nô bởi công thức \(v = 5\sqrt l \).
a) Một ca nô để lại đường sóng nước sau đuôi dài 4 m thì tốc độ của nó là bao nhiều kilômét trên giờ.
b) Khi ca nó di chuyển với tốc độ 54 km/h thì đường sóng nước sau đuôi dài bao nhiêu mét?
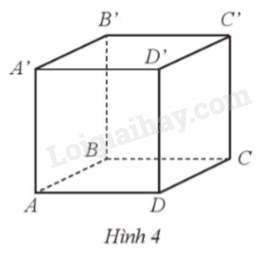
Một chất điểm di chuyển từ định A' đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?







Danh sách bình luận