Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng \(2\,{m^2}.\) Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét?

Tìm các số $x$ không âm thỏa mãn $\sqrt x  \ge 3$

Cho biểu thức \(C = \sqrt {2x - 1} .\)

a) Tính giá trị của biểu thức tại \(x = 5.\)

b) Tại \(x = 0\) có tính được giá trị của biểu thức không? Vì sao?

Cho căn thức \(\sqrt {5 - 2x} .\)

a) Tìm điều kiện xác định của căn thức.

b) Tính giá trị của căn thức tại \(x = 2.\)

Trở lại tình huống mở đầu.

Tình huống mở đầu

Trong Vật lí, quãng đường S (tính bằng mét) của một vật tự rơi tự do được cho bởi công thức \(S = 4,9{t^2},\) trong đó t là thời gian rơi (tính bằng giây) . Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?

a) Viết công thức tính thời gian t (giây) cần thiết để vật rơi được quãng đường S (mét)

b) Sử dụng công thức tìm được trong câu a, hãy trả lời câu hỏi trong tình huống mở đầu

Tìm điều kiện xác định của \(\sqrt {x + 10} \) và tính giá trị của căn thức tại \(x =  - 1.\)

Kích thước màn hình ti vi hình chữ nhật được xác định bởi độ dài đường chéo. Một loại ti vi có tỉ lệ hai cạnh màn hình là 4:3.

a) Gọi x (inch) là chiều rộng của màn hình tivi. Viết công thức tính độ dài đường chéo d (inch) của màn hình ti vi theo x.

b) Tính chiều rộng và chiều dài (theo centimet) của màn hình ti vi loại 40 inch.

Chứng minh rằng:

a) \({\left( {1 - \sqrt 2 } \right)^2} = 3 - 2\sqrt 2 ;\)

b) \({\left( {\sqrt 3  + \sqrt 2 } \right)^2} = 5 + 2\sqrt 6 .\)

Trong Vật lí, tốc độ (m/s) của một vật đang bay được cho bởi công thức \(v = \sqrt {\frac{{2E}}{m}} ,\) trong đó E là động năng của vật (tính bằng Joule, kí hiệu là J) và m (kg) là khối lượng của vật (Theo sách Vật lí đại cương, NXB Giáo dục Việt Nam, 2016) .

Tính tốc độ bay của một vật khi biết vật đó có khối lượng 2,5 kg và động năng 281,25 J.

Với giá trị nào của x thì biểu thức A = \(\sqrt {3x + 6} \) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai).

Cho biểu thức P = \(\sqrt {{a^2} - {b^2}} \). Tính giá trị của P khi:

a) a = 5; b = 0

b) a = 5; b = -5

c) a = 2; b = -4

Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)

a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.

b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).

Tính giá trị của các biểu thức:

a) \({\left( {\sqrt {5,25} } \right)^2} + {\left( { - \sqrt {1,75} } \right)^2}\)

b) \({\left( {\sqrt {102} } \right)^2} - \sqrt {{{98}^2}} \)

Tính giá trị của các biểu thức sau khi x = 16; y = 9

a) \(\sqrt x  + \sqrt y \)

b) \(\sqrt {x + y} \)

c) \(\frac{1}{2}\sqrt {xy} \)

d) \(\frac{1}{6}x\sqrt y \)

Cho biểu thức P = \(\sqrt {{x^2} - xy + 1} \). Tính giá trị của P khi:

a) x = 3; y = - 2

b) x = 1; y = 4

Kết quả của phép tính \(\sqrt {27} :\sqrt 6 .2\sqrt {18} \) là

A. 12

B. 18

C. 72

D. 144

Tìm các số \(x\) không âm thỏa mãn \(\sqrt {5x}  < 10\)

Tìm giá trị của $x$ không âm biết $2\sqrt x  - 30 = 0$.

Tìm giá trị của \(x\) không âm biết \(5\sqrt {2x}  - 125 = 0\).

Khẳng định nào sau đây đúng  về nghiệm ${x_0}$ của phương trình  \(\dfrac{{9x - 7}}{{\sqrt {7x + 5} }} = \sqrt {7x + 5} \)

Tính giá trị biểu thức \(A = \dfrac{1}{{1 + \sqrt 3 }} + \dfrac{1}{{\sqrt 3  + \sqrt 5 }} + \dfrac{1}{{\sqrt 5  + \sqrt 7 }} \)\(+ ... + \dfrac{1}{{\sqrt {2019}  + \sqrt {2021} }}\)

Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{{x + \sqrt x  + 4}}{{\sqrt x }}\) với \(x > 0\)

Cho \(A = \dfrac{1}{{\sqrt 3  - 1}} - \sqrt {27}  + \dfrac{3}{{\sqrt 3 }};\)\(B = \dfrac{{5 + \sqrt 5 }}{{\sqrt 5  + 2}} + \dfrac{{\sqrt 5 }}{{\sqrt 5  - 1}} - \dfrac{{3\sqrt 5 }}{{3 + \sqrt 5 }}\). Chọn câu đúng.

Tính giá trị của \(A =\dfrac{1}{{2\sqrt 1  + 1\sqrt 2 }} + \dfrac{1}{{3\sqrt 2  + 2\sqrt 3 }} + ... + \dfrac{1}{{2018\sqrt {2017}  + 2017\sqrt {2018} }}\)

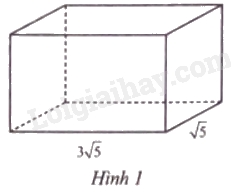
Cho hình hộp chữ nhật với chiều dài \(3\sqrt 5 \) cm, chiều rộng \(\sqrt 5 \) cm và thể tích \(30\sqrt 5 \) cm³ như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó.

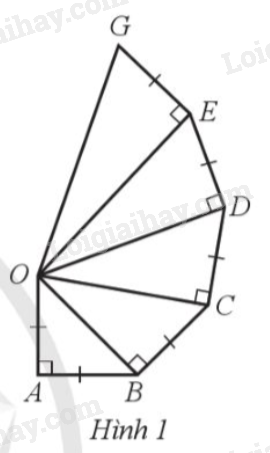
Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\)

Trên một đoạn sông, tốc độ dòng chảy của nước ở bề mặt sông lớn hơn tốc độ dòng chảy của nước ở đáy sông. Gọi v (km/h) là tốc độ dòng chảy của nước ở bề mặt sông và f (km/h) là tốc độ dòng chảy của nước ở đây sông. Khi đó, ta có công thức: \(\sqrt f  = \sqrt v  - 1,3\).

a) Tính tốc độ dòng chảy của nước ở đáy sông, biết tốc độ dòng chảy của nước ở bề mặt sông là 9 km/h.

b) Tính tốc độ dòng chảy của nước ở bề mặt sông, biết tốc độ dòng chảy của nước ở đáy sông là 20,25 km h.

Tính giá trị của mỗi biểu thức:

a) \(\sqrt {2x + 7} \) với \(x = 1;x = \frac{2}{3};x = 2\sqrt 3 .\)

b) \(\sqrt { - {x^2} + 2x + 11} \) với \(x = 0;x = \frac{1}{2};x = \sqrt 5 .\)

c) \(\sqrt[3]{{{x^3} + 3{x^2} + 3x + 1}}\) với \(x =  - 1;x =  - \frac{1}{3};x = \sqrt 2 .\)

Điện áp U (V) yêu cầu cho một mạch điện được cho bởi công thức \(U = \sqrt {P.R} \), trong đó P (W) là công suất tiêu thụ của điện trở và R (Ω) là giá trị điện trở.

a) Tính điện áp để thắp sáng cho bóng đèn A có công suất tiêu thụ là 100 W và giá trị điện trở là 110 Ω (làm tròn kết quả đến hàng đơn vị của vôn).

b) Bóng đèn B có điện áp 110 V và giá trị điện trở là 88 Ω. Công suất tiêu thụ của bóng đèn B có lớn hơn công suất tiêu thụ của bóng đèn A hay không? Vì sao?

Tốc độ v (m/s) của một chiếc ca nô được tính theo độ dài đường sóng nước sau đuôi \(l\) (m) của ca nô bởi công thức \(v = 5\sqrt l \).

a) Một ca nô để lại đường sóng nước sau đuôi dài 4 m thì tốc độ của nó là bao nhiều kilômét trên giờ.

b) Khi ca nó di chuyển với tốc độ 54 km/h thì đường sóng nước sau đuôi dài bao nhiêu mét?

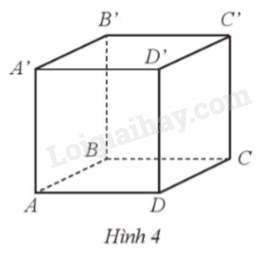
Một chất điểm di chuyển từ định A' đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?