Cho p và p+4 là các số nguyên tố(p>3). Chứng tỏ rằng p+8 là hợp số.
Xét các trường hợp
Vì p là số nguyên tố, p> 3 nên khi p chia cho 3 xảy ra các trường hợp là chia cho 3 dư 1 hoặc dư 2
+Trường hợp 1: p chia cho 3 dư 1 thì p+8 chia hết cho 3 nên p+8 là hợp số
+Trường hợp 2: p chia cho 3 dư 2 thì p+4 chia hết cho 3, mà p+4>3 nên p+4 không là số nguyên tố.(không thỏa mãn)
Vậy nếu p và p+4 là các số nguyên tố(p>3) thì p+8 là hợp số.
Các bài tập cùng chuyên đề
Kiểm tra xem các số sau là số nguyên tố hay hợp số bằng cách dùng dấu hiệu chia hết hoặc tra bảng số nguyên tố:
89; 97; 125; 541; 2013; 2018.
Em hãy tìm nhà thích hợp cho các số trong bảng 2.1.
Trong các số cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
a) 1 930;
b) 23.
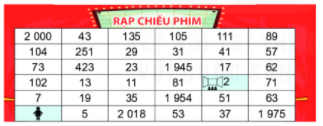
Bạn Hà đang ở ô tìm đường đến phòng chiếu phim 2. Biết rằng chỉ có thể đi từ một ô sang ở chung cạnh có chứa số nguyên tố. Em hãy giúp Hà đến được phòng chiếu phim nhé.
Mỗi số sau là số nguyên tố hay hợp số? Giải thích.
a) 213;
b) 245;
c) 3737;
d) 67.
Bình dùng một khay hình vuông cạnh 60 cm để xếp bánh chưng. Mỗi chiếc bánh chưng hình vuông có cạnh 15 cm. Bình có thể dùng những chiếc bánh chưng để xếp vừa khít vào khay này không? Giải thích.
a) Tìm tất cả các ước của các số từ 1 đến 10.
b) Sắp xếp các số từ 1 đến 10 thành ba nhóm:
- Nhóm 1 bao gồm các số chỉ có một ước.
- Nhóm 2 bao gồm các số chỉ có hai ước khác nhau.
- Nhóm 3 bao gồm các số có nhiều hơn hai ước khác nhau.
a) Trong các số 11; 12; 25, số nào là số nguyên tố, số nào là hợp số? Vì sao?
b) Lan nói rằng: “Nếu một số tự nhiên không là số nguyên tố thì nó phải là hợp số. Em có đồng ý với Lan không? Vì sao?
Bác Vĩnh mua 17 cuốn sổ và 34 chiếc bút để làm quà tặng. Bác Vĩnh muốn chia đều 17 cuốn sổ thành các gói và cũng muốn chia đều 34 chiếc bút thành các gói. Bác Vĩnh có bao nhiêu cách chia những cuốn sổ thành các gói? Có bao nhiêu cách chia những chiếc bút thành các gói?
Cho các số 36, 37, 69, 75. Trong các số đó:
a) Số nào là nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Mỗi phát biểu sau đúng hay sai? Vì sao?
a) Mỗi số tự nhiên không là số nguyên tố thì sẽ là hợp số.
b) Mọi số nguyên tố đều là số lẻ.
c) 3 là ước nguyên tố của 6 nên 3 cũng là ước nguyên tố của 18.
d) Mọi số tự nhiên đều có ước số nguyên tố.
Thay chữ số thích hợp vào dấu * để được mỗi số sau là:
a) hợp số: \(\overline {2*} ;\overline {3*} \)
b) số nguyên tố: \(\overline {1*} ;\overline {4*} \)
a) Điền “Đ” (đúng), “S”(sai) vào các ô trống cho mỗi kết luận trong bảng sau:
|
Kết luận |
Đ/S |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
|
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
|
|
iii. Tổng của hai hợp số luôn là một hợp số. |
|
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
|
b) Với mỗi kết luận sai trong câu a, hãy cho ví dụ minh hoạ.
1) Thực hiện các phép tính:
a) 25 . 8 – 15 . 5 + 160 : 16 – 10;
b) 2 . 52 – 3 : 710 + 54 : 33.
2) Phân tích các số 84, 120, 210 ra thừa số nguyên tố.
Tìm chữ số a để
a)\(\overline {49a} \) là số nguyên tố
b)\(\overline {23a} \) là hợp số
Kiểm tra xem trong các số sau, số nào là số nguyên tố, số nào là hợp số bằng cách dùng dấu hiệu chia hết hoặc tra bảng số nguyên tố:
829; 971; 9 891; 12 344; 32 015.
Cho các số 3, 13, 17, 18, 25, 39, 41. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Tìm chữ số x để mỗi số sau là hợp số:
a) \(\overline {2x} \)
b) \(\overline {7x} \)
Tổng sau là số nguyên tố hay hợp số?
a) \(8.9.10 + 11.12;\)
b) \(11.13.15 + 2021.2023.\)
Số 2021 có thể viết thành tổng của hai số nguyên tố được không? Vì sao?
Trong các khẳng định sau, khẳng định sai là:
Hãy chọn phát biểu SAI:
