Muốn trục căn thức ở mẫu của biểu thức \(\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 2 - 1}}\) ta cần:
A. Nhân biểu thức đó với \(\left( {\sqrt 3 - \sqrt 2 } \right)\).
B. Nhân biểu thức đó với \(\left( {\sqrt 2 + 1} \right)\).
C. Nhân biểu thức đó với biểu thức liên hợp.
D. Nhân cả tử và mẫu của biểu thức đó với \(\left( {\sqrt 2 - 1} \right)\).
Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\) ta có \(\frac{C}{{\sqrt A - B}} = \frac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\)
Muốn trục căn thức ở mẫu của biểu thức \(\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 2 - 1}}\) ta cần nhân cả tử và mẫu của biểu thức đó với\(\left( {\sqrt 2 + 1} \right)\).
Không có đáp án đúng

Các bài tập cùng chuyên đề
Cho hai biểu thức \(\frac{{ - 2}}{{\sqrt 3 + 1}}\) và \(\frac{1}{{\sqrt 3 - \sqrt 2 }}.\) Hãy thực hiện các yêu cầu sau để viết các biểu thức đó dưới dạng không có căn thức ở mẫu:
a) Xác định biểu thức liên hợp của mẫu.
b) Nhân cả tử và mẫu với biểu thức liên hợp của mẫu.
c) Sử dụng hằng đẳng thức hiệu hai bình phương để rút gọn mẫu của biểu thức nhận được.
Nhân cả tử và mẫu của biểu thức \(\frac{{3a}}{{2\sqrt 2 }}\) với \(\sqrt 2 \) và viết biểu thức nhận được dưới dạng không có căn thức ở mẫu.
Rút gọn biểu thức sau:
\(\left( {\frac{{\sqrt {22} - \sqrt {11} }}{{1 - \sqrt 2 }} + \frac{{\sqrt {21} - \sqrt 7 }}{{1 - \sqrt 3 }}} \right)\left( {\sqrt 7 - \sqrt {11} } \right).\)
Trục căn thức ở mẫu:
a) \(\frac{{4 + 3\sqrt 5 }}{{\sqrt 5 }};\)
b) \(\frac{1}{{\sqrt 5 - 2}};\)
c) \(\frac{{3 + \sqrt 3 }}{{1 - \sqrt 3 }};\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}.\)
Không sử dụng MTCT, tính giá trị của biểu thức \(A = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4{{\left( {2 + \sqrt 3 } \right)}^2}} - \frac{1}{{2 - \sqrt 3 }}.\)
Bốn ô cửa hình vuông diện tích \(\frac{1}{2}{m^2}\) ghép thành cửa sổ Hình 1.
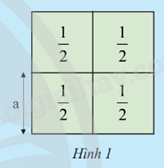
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Kết quả của mỗi bạn có đúng không? Giải thích?
b) Biết rằng \(\sqrt 2 \approx 1,4142\). Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.

Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }}\)
b) \( - \frac{{10}}{{3\sqrt 5 }}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\)
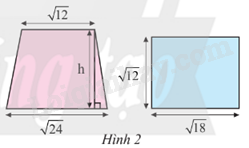
Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.
Trục căn thức ở mẫu: \(\frac{{x_{}^2 - 1}}{{\sqrt {x - 1} }}\) với \(x > 1\).
Trục căn thức ở mẫu: \(\frac{{x - 1}}{{\sqrt x - 1}}\) với \(x > 1\).
Trục căn thức ở mẫu: \(\frac{1}{{\sqrt {x + 1} - \sqrt x }}\) với \(x \ge 0\).
a) Nhân cả tử và mẫu của biểu thức \(\frac{4}{{3\sqrt 2 }}\) với \(\sqrt 2 \) rồi biến đổi biểu thức đó về dạng không còn căn thức ở mẫu.
b) Nhân cả tử và mẫu của biểu thức \(\frac{5}{{\sqrt 2 + 1}}\) với \(\sqrt 2 - 1\) rồi biến đổi biểu thức đó về dạng không còn căn thức ở mẫu.
c) Nhân cả tử và mẫu của biểu thức \(\frac{6}{{\sqrt 5 - \sqrt 2 }}\) với \(\sqrt 5 + \sqrt 2 \) rồi biến đổi biểu thức đó về dạng không còn căn thức ở mẫu.
Giá trị của biểu thức \(\frac{1}{{3 + \sqrt 5 }} + \frac{1}{{3 - \sqrt 5 }}\) là
A. \(\frac{3}{2}\).
B. \(\frac{1}{3}\).
C. \(\frac{1}{6}\).
D. \(\frac{1}{2}\).
Thực hiện phép tính \(\sqrt {\frac{{3 - 2\sqrt 2 }}{{17 - 12\sqrt 2 }}} - \sqrt {\frac{{3 + 2\sqrt 2 }}{{17 + 12\sqrt 2 }}} \).
Không sử dụng MTCT, chứng minh rằng biểu thức sau có giá trị là một số nguyên:
\(P = \left( {\frac{{\sqrt 5 + 1}}{{1 + \sqrt 5 + \sqrt 3 }} + \frac{{\sqrt 5 - 1}}{{1 + \sqrt 3 - \sqrt 5 }}} \right)\left( {\sqrt 3 - \frac{4}{{\sqrt 3 }} + 2} \right).\sqrt {0,2}. \)
Độ dài đường chéo của một hình vuông lớn hơn độ dài cạnh của nó là 4 cm. Tính độ dài cạnh của hình vuông đó.
a) Chứng minh rằng \(\frac{1}{{\sqrt {n + 1} + \sqrt n }} = \sqrt {n + 1} - \sqrt n \) với mọi số tự nhiên n.
b) Tính \(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {99} + \sqrt {100} }}.\)
Giá trị của biểu thức \(\frac{1}{{\sqrt 3 + \sqrt 2 }} - \frac{1}{{\sqrt 3 - \sqrt 2 }}\) bằng:
A. 0
B. 4
C. \(2\sqrt 2 \)
D. \( - 2\sqrt 2 \)
Tốc độ lăn \(v(m/s)\) của vật thể có khối lượng m (kg) chịu tác động từ lực Ek được cho bởi công thức \(v = \sqrt {\frac{{2{E_k}}}{m}} \).
a) Tính tốc độ lăn của quả bóng nặng 3kg khi một người tác động lực Ek = 18J lên quả bóng.
b) Muốn lăn của quả bóng nặng 3kg với tốc độ 6m/s thì cần tác động lực bao nhiêu jun lên quả bóng đó?
Trục căn thức ở mẫu:
a) \(\frac{{4 + 3\sqrt 5 }}{{\sqrt 5 }}\);
b) \(\frac{1}{{\sqrt 5 - 2}}\);
c) \(\frac{{3 + \sqrt 3 }}{{1 - \sqrt 3 }}\);
d) \(\frac{{\sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\).







Danh sách bình luận