Cho \(a = \sqrt {3 - 2\sqrt 2 } \) và \(b = \sqrt {3 + 2\sqrt 2 } \). Chứng minh:
a) \(a - b\) là một số nguyên.
b) \(ab\) là một số tự nhiên.
Bước 1: Biến đổi \(3 - 2\sqrt 2 \) và \(3 + 2\sqrt 2 \) thành bình phương của một hiệu và một tổng.
Bước 2: Rút gọn các biểu thức \(a - b\) và \(ab\).
a) \(a - b \) \(= \sqrt {3 - 2\sqrt 2 } - \sqrt {3 + 2\sqrt 2 } \) \(= \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} - \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} \) \(= \left| {\sqrt 2 - 1} \right| - \left| {\sqrt 2 + 1} \right| \) \(= \left( {\sqrt 2 - 1} \right) - \left( {\sqrt 2 + 1} \right) \) \(= - 2.\)
Vậy \(a - b\) là một số nguyên.
b) \(a.b \) \(= \sqrt {3 - 2\sqrt 2 } .\sqrt {3 + 2\sqrt 2 } \) \(= \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} .\sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} \) \(= \left| {\sqrt 2 - 1} \right|.\left| {\sqrt 2 + 1} \right|\\ \) \(= \left( {\sqrt 2 - 1} \right).\left( {\sqrt 2 + 1} \right) \) \(= {\left( {\sqrt 2 } \right)^2} - 1 \) \(= 2 - 1 \) \(= 1.\)
Vậy \(ab\) là một số tự nhiên.

Các bài tập cùng chuyên đề
So sánh:
a) \(\sqrt 5 .\sqrt {11} \) và \(\sqrt {56} \);
b) \(\frac{{\sqrt {141} }}{{\sqrt 3 }}\) và 7.
Không dùng MTCT, tính giá trị của các biểu thức sau:
a) \(\sqrt {1\frac{2}{3}} :\sqrt {\frac{1}{{15}}} \);
b) \(\sqrt {4,9} .\sqrt {1\;000} \).
Không dùng MTCT, chứng minh rằng các biểu thức sau có giá trị là số nguyên:
a) \(\sqrt {8 + \sqrt {15} } .\sqrt {8 - \sqrt {15} } \);
b) \({\left( {\sqrt {6 - \sqrt {11} } + \sqrt {6 + \sqrt {11} } } \right)^2}\).
Thực hiện phép tính \({\left( {\frac{1}{{\sqrt 8 + \sqrt 7 }} + \sqrt {175} - 2\sqrt 2 } \right)^2}\).
a) \(\sqrt {24} :\sqrt 2 .\sqrt 3 \)
b) \(\sqrt {27} .\sqrt {50} :\sqrt 6 \)
c) \(\sqrt {32} :\frac{{2\sqrt 2 }}{{\sqrt 5 }}:\left( { - \sqrt {45} } \right)\)
d) \(\frac{{\sqrt {8,5} .\sqrt {15,3} }}{{\sqrt {0,45} }}\)
So sánh:
a) \(\frac{{\sqrt {1404} }}{{\sqrt {351} }}\) và \(\sqrt {\frac{{98}}{{25}}} \)
b) \(\frac{5}{2}\sqrt {\frac{1}{6}} \) và \(6\sqrt {\frac{1}{{35}}} \)
c) \( - 5\sqrt 8 \) và \( - \sqrt {190} \)
d) 16 và \(\sqrt {15} .\sqrt {17} \)
Cho các biểu thức \(A = \frac{{\sqrt {{{35}^3} + 1} }}{{\sqrt {{{35}^2} - 34} }};B = \left( {\frac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 - \sqrt 5 }}\)
Chứng minh \(A = 6;B = - 2.\)
Rút gọn biểu thức:
a) \(\sqrt {20} - \sqrt {45} + \sqrt 5 \)
b) \({\left( {\sqrt 6 - \sqrt 5 } \right)^2} + \sqrt {120} \)
c) \(\left( {3\sqrt 5 + \sqrt {13} } \right)\left( {\sqrt {45} - \sqrt {13} } \right)\)
d) \(\left( {2\sqrt 3 + \sqrt 5 } \right)\sqrt 3 - \sqrt {60} \)
Trong Hình 1, biết hai hình vuông có diện tích lần lượt là 108 cm2 và 96 cm2. Diện tích của hình chữ nhật ABCD là
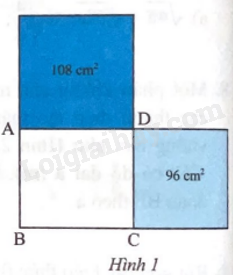
A. \(48\sqrt 3 \) cm2
B. \(24\sqrt 6 \) cm2
C. \(72\sqrt 2 \) cm2
D. 144 cm2
Rút gọn biểu thức \(\frac{{\sqrt {20} }}{{\sqrt {24} }}.\frac{{\sqrt 8 }}{{\sqrt {10} }}:\left( { - \sqrt {\frac{2}{9}} } \right)\), ta có kết quả
A. \( - \sqrt 2 \)
B. \( - \frac{{3\sqrt 2 }}{2}\)
C. \( - \frac{{2\sqrt 3 }}{3}\)
D. \( - \sqrt 3 \)
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
a) Chiều dài của cạnh AB là \(2\sqrt 2 \) m.
b) Chênh lệch chiều dài giữa hai cạnh AB và CD là \(\sqrt {10} \) m.
c) Diện tích của bức tường là \(10\sqrt 6 \) m2.
d) Chiều dài cạnh AD là \(\sqrt {26} \)m.
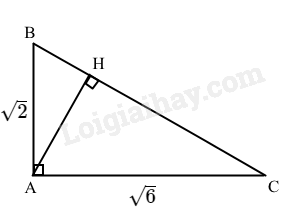
Cho tam giác ABC vuông tại A, \(AB = \sqrt 2 ,AC = \sqrt 6 \). Tính giá trị đúng (không làm trò) của
a) Chu vi và diện tích tam giác ABC.
b) Độ dài đường cao AH của tam giác ABC.
So sánh:
a) \(5\sqrt 5 \) và \(4\sqrt 3 \)
b) \(\sqrt {36 + 16} \) và \(\sqrt {36} + \sqrt {16} \)
c) \(\frac{1}{{\sqrt {60} }}\) và \(2\sqrt {\frac{1}{{15}}} \)
d) \(\sqrt 6 - \sqrt 2 \) và 1
Tìm x, biết:
a) \(\frac{5}{3}\sqrt {15x} - \sqrt {15x} - 2 = \frac{1}{3}\sqrt {15x} \) với \(x \ge 0\).
b) \(\sqrt {9{x^2}} = \left| { - 18} \right|\) với \(x \ge 0\).
c) \({x^2} - 8 = 0\)
d) \(\sqrt {{x^2} - 49} - \sqrt {x - 7} = 0\) với \(x \ge 7\)
Xét 4 khẳng định sau:
(1) \(\sqrt {{a^2}{b^2}} = \left| {ab} \right|\), (a, b tùy ý);
(2) \(\sqrt {{a^2}{b^2}} = ab\), (a, b tùy ý);
(3) \(\sqrt {{a^2}{b^2}} = \left| a \right|\left| b \right|\), (a, b tùy ý);
(4) \(\sqrt {{a^2}{b^2}} = \left( { - a} \right)\left( { - b} \right)\), (a, b tùy ý);
Trong 4 khẳng định trên, số khẳng định đúng là:
A. 1.
B. 2.
C. 3.
D. 4.
Thực hiện phép tính:
a) \(\sqrt 3 \left( {\sqrt {192} - \sqrt {75} } \right)\);
b) \(\frac{{ - 3\sqrt {18} + 5\sqrt {50} - \sqrt {128} }}{{7\sqrt 2 }}\).
Chứng minh rằng:
a) \({\left( {1 - \sqrt 2 } \right)^2} = 3 - 2\sqrt 2 \);
b) \({\left( {\sqrt 3 + \sqrt 2 } \right)^2} = 5 + 2\sqrt 6 \).







Danh sách bình luận