Cho các biểu thức \(A = \frac{{\sqrt {{{35}^3} + 1} }}{{\sqrt {{{35}^2} - 34} }};B = \left( {\frac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 - \sqrt 5 }}\)
Chứng minh \(A = 6;B = - 2.\)
Biểu thức A: Áp dụng hằng đẳng thức \({a^3} + {b^3}\) với \({35^3} + 1\).
Biểu thức B: Biến đổi \(\frac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }} = \frac{{\sqrt 7 \left( {\sqrt 2 - 1} \right)}}{{1 - \sqrt 2 }} + \frac{{\sqrt 5 \left( {\sqrt 3 - 1} \right)}}{{1 - \sqrt 3 }} = - \sqrt 7 - \sqrt 5 \).
\(A = \frac{{\sqrt {{{35}^3} + 1} }}{{\sqrt {{{35}^2} - 34} }} = \frac{{\sqrt {\left( {35 + 1} \right)\left( {{{35}^2} - 35 + 1} \right)} }}{{\sqrt {{{35}^2} - 34} }}\\= \frac{{\sqrt {36\left( {{{35}^2} - 34} \right)} }}{{\sqrt {{{35}^2} - 34} }} = \sqrt {36} = 6.\)
Vậy \(A = 6\).
\(\begin{array}{l}B = \left( {\frac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 - \sqrt 5 }} \\= \left( {\frac{{\sqrt 7 \left( {\sqrt 2 - 1} \right)}}{{1 - \sqrt 2 }} + \frac{{\sqrt 5 \left( {\sqrt 3 - 1} \right)}}{{1 - \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 - \sqrt 5 }}\\ = \left( { - \sqrt 7 - \sqrt 5 } \right).\left( {\sqrt 7 - \sqrt 5 } \right)\\= - \left( {\sqrt 7 + \sqrt 5 } \right).\left( {\sqrt 7 - \sqrt 5 } \right) \\= - \left[ {{{\left( {\sqrt 7 } \right)}^2} - {{\left( {\sqrt 5 } \right)}^2}} \right]\\ = - \left( {7 - 5} \right) = - 2\end{array}\)
Vậy \(B = - 2\).

Các bài tập cùng chuyên đề
So sánh:
a) \(\sqrt 5 .\sqrt {11} \) và \(\sqrt {56} \);
b) \(\frac{{\sqrt {141} }}{{\sqrt 3 }}\) và 7.
Không dùng MTCT, tính giá trị của các biểu thức sau:
a) \(\sqrt {1\frac{2}{3}} :\sqrt {\frac{1}{{15}}} \);
b) \(\sqrt {4,9} .\sqrt {1\;000} \).
Không dùng MTCT, chứng minh rằng các biểu thức sau có giá trị là số nguyên:
a) \(\sqrt {8 + \sqrt {15} } .\sqrt {8 - \sqrt {15} } \);
b) \({\left( {\sqrt {6 - \sqrt {11} } + \sqrt {6 + \sqrt {11} } } \right)^2}\).
Thực hiện phép tính \({\left( {\frac{1}{{\sqrt 8 + \sqrt 7 }} + \sqrt {175} - 2\sqrt 2 } \right)^2}\).
a) \(\sqrt {24} :\sqrt 2 .\sqrt 3 \)
b) \(\sqrt {27} .\sqrt {50} :\sqrt 6 \)
c) \(\sqrt {32} :\frac{{2\sqrt 2 }}{{\sqrt 5 }}:\left( { - \sqrt {45} } \right)\)
d) \(\frac{{\sqrt {8,5} .\sqrt {15,3} }}{{\sqrt {0,45} }}\)
So sánh:
a) \(\frac{{\sqrt {1404} }}{{\sqrt {351} }}\) và \(\sqrt {\frac{{98}}{{25}}} \)
b) \(\frac{5}{2}\sqrt {\frac{1}{6}} \) và \(6\sqrt {\frac{1}{{35}}} \)
c) \( - 5\sqrt 8 \) và \( - \sqrt {190} \)
d) 16 và \(\sqrt {15} .\sqrt {17} \)
Rút gọn biểu thức:
a) \(\sqrt {20} - \sqrt {45} + \sqrt 5 \)
b) \({\left( {\sqrt 6 - \sqrt 5 } \right)^2} + \sqrt {120} \)
c) \(\left( {3\sqrt 5 + \sqrt {13} } \right)\left( {\sqrt {45} - \sqrt {13} } \right)\)
d) \(\left( {2\sqrt 3 + \sqrt 5 } \right)\sqrt 3 - \sqrt {60} \)
Cho \(a = \sqrt {3 - 2\sqrt 2 } \) và \(b = \sqrt {3 + 2\sqrt 2 } \). Chứng minh:
a) \(a - b\) là một số nguyên.
b) \(ab\) là một số tự nhiên.
Trong Hình 1, biết hai hình vuông có diện tích lần lượt là 108 cm2 và 96 cm2. Diện tích của hình chữ nhật ABCD là
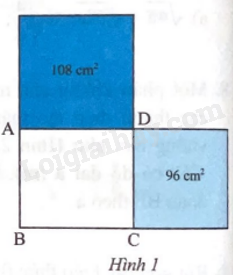
A. \(48\sqrt 3 \) cm2
B. \(24\sqrt 6 \) cm2
C. \(72\sqrt 2 \) cm2
D. 144 cm2
Rút gọn biểu thức \(\frac{{\sqrt {20} }}{{\sqrt {24} }}.\frac{{\sqrt 8 }}{{\sqrt {10} }}:\left( { - \sqrt {\frac{2}{9}} } \right)\), ta có kết quả
A. \( - \sqrt 2 \)
B. \( - \frac{{3\sqrt 2 }}{2}\)
C. \( - \frac{{2\sqrt 3 }}{3}\)
D. \( - \sqrt 3 \)
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
a) Chiều dài của cạnh AB là \(2\sqrt 2 \) m.
b) Chênh lệch chiều dài giữa hai cạnh AB và CD là \(\sqrt {10} \) m.
c) Diện tích của bức tường là \(10\sqrt 6 \) m2.
d) Chiều dài cạnh AD là \(\sqrt {26} \)m.
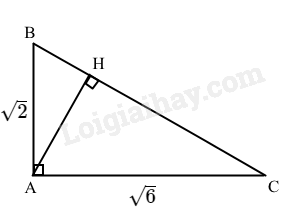
Cho tam giác ABC vuông tại A, \(AB = \sqrt 2 ,AC = \sqrt 6 \). Tính giá trị đúng (không làm trò) của
a) Chu vi và diện tích tam giác ABC.
b) Độ dài đường cao AH của tam giác ABC.
So sánh:
a) \(5\sqrt 5 \) và \(4\sqrt 3 \)
b) \(\sqrt {36 + 16} \) và \(\sqrt {36} + \sqrt {16} \)
c) \(\frac{1}{{\sqrt {60} }}\) và \(2\sqrt {\frac{1}{{15}}} \)
d) \(\sqrt 6 - \sqrt 2 \) và 1
Tìm x, biết:
a) \(\frac{5}{3}\sqrt {15x} - \sqrt {15x} - 2 = \frac{1}{3}\sqrt {15x} \) với \(x \ge 0\).
b) \(\sqrt {9{x^2}} = \left| { - 18} \right|\) với \(x \ge 0\).
c) \({x^2} - 8 = 0\)
d) \(\sqrt {{x^2} - 49} - \sqrt {x - 7} = 0\) với \(x \ge 7\)
Xét 4 khẳng định sau:
(1) \(\sqrt {{a^2}{b^2}} = \left| {ab} \right|\), (a, b tùy ý);
(2) \(\sqrt {{a^2}{b^2}} = ab\), (a, b tùy ý);
(3) \(\sqrt {{a^2}{b^2}} = \left| a \right|\left| b \right|\), (a, b tùy ý);
(4) \(\sqrt {{a^2}{b^2}} = \left( { - a} \right)\left( { - b} \right)\), (a, b tùy ý);
Trong 4 khẳng định trên, số khẳng định đúng là:
A. 1.
B. 2.
C. 3.
D. 4.
Thực hiện phép tính:
a) \(\sqrt 3 \left( {\sqrt {192} - \sqrt {75} } \right)\);
b) \(\frac{{ - 3\sqrt {18} + 5\sqrt {50} - \sqrt {128} }}{{7\sqrt 2 }}\).
Chứng minh rằng:
a) \({\left( {1 - \sqrt 2 } \right)^2} = 3 - 2\sqrt 2 \);
b) \({\left( {\sqrt 3 + \sqrt 2 } \right)^2} = 5 + 2\sqrt 6 \).







Danh sách bình luận