Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - {y^2} + 8x - 8y\);

b) \(4{x^2} + 4xy + {y^2} - 4x - 2y\);

c) \({x^3} + {y^3} + 4x + 4y\);

d) \({x^3} - 3{x^2}y + 3x{y^2} - {y^3} + {x^2} - {y^2}\);

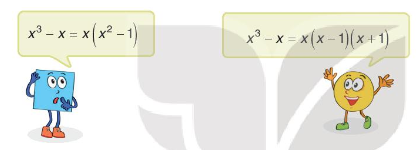
Phân tích đa thức \({x^3} - x\) thành nhân tử.

Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.

Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a)\,{x^2} + xy;\\b)\,6{a^2}b - 18ab;\\c)\,{x^3} - 4x;\\d)\,{x^4} - 8x.\end{array}\)

Phân tích các đa thức sau thành nhân tử:

a)      \({x^2} - 9 + xy + 3y\)

b)      \({x^2}y + {x^2} + xy - 1\)

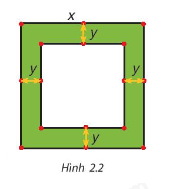
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)

a)      Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b)      Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.

Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a)\,{x^2} - 6x + 9 - {y^2};\\b)\,4{x^2} - {y^2} + 4y - 4;\\c)\,xy + {z^2} + xz + yz;\\d)\,{x^2} - 4xy + 4{y^2} + xz - 2yz.\end{array}\)

Phân tích các đa thức sau thành nhân tử:

a)      \({x^3} + {y^3} + x + y\)

b)      \({x^3} - {y^3} + x - y\)

c)      \({\left( {x - y} \right)^3} + {\left( {x + y} \right)^3}\)

d)      \({x^3} - 3{x^2}y + 3x{y^2} - {y^3} + {y^2} - {x^2}\)

Rút gọn các biểu thức:

a)      \(\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\)

b)      \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\)

Phân tích các đa thức sau thành nhân tử:

a)      \(6{x^2} - 24{y^2}\)

b)      \(64{x^3} - 27{y^3}\)

c)      \({x^4} - 2{x^3} + {x^2}\)

d)      \({\left( {x - y} \right)^3} + 8{y^3}\)

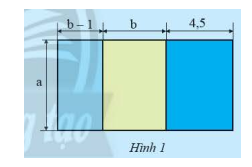
Tính diện tích của nền nhà có bản vẽ sơ lượng như Hình 1 theo những cách khác nhau, biết \(a = 5\); \(b = 3,5\) (các kích thước tính theo mét). Tính theo cách nào nhanh hơn?

Tìm một hình hộp chữ nhật có thể tích \(2{x^3} - 18x\) với (\(x > 3\)) mà độ dài các cạnh đều là biểu thức chứa \(x\).

Giải đáp câu hỏi mở đầu (trang 23)

Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:

\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)

Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Phân tích các đa thức sau thành nhân tử:

a) \({a^3} - {a^2}b + a - b\)                                                  

b) \({x^2} - {y^2} + 2y - 1\)

Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết \(a = 0,8\); \(b = 2\) (các kích thước tính theo mét).

Phân tích các đa thức sau thành nhân tử:

a) \(4{x^3} - 16x\)

b) \({x^4} - {y^4}\)

c) \(x{y^2} + {x^2}y + \dfrac{1}{4}{y^3}\)

d) \({x^2} + 2x - {y^2} + 1\)

Khi phân tích đa thức \(P = {x^4} - 4{x^2}\) thành nhân tử thì được:

A. \(P = {x^2}(x - 2)(x + 2)\)   

B. \(P = x(x - 2)(x + 2)\)

C. \(P = {x^2}(x - 4)(x + 4)\)  

D. \(P = x(x - 4)(x + 2)\)

Phân tích các đa thức sau thành nhân tử:

a) \({\left( {x - 1} \right)^2} - 4\) 

b) \(4{x^2} + 12x + 9\) 

c) \({x^3} - 8{y^6}\)

d) \({x^5} - {x^3} - {x^2} + 1\) 

e) \( - 4{x^3} + 4{x^2} + x - 1\) 

f) \(8{x^3} + 12{x^2} + 6x + 1\)

Bác Hoa gửi tiết kiệm a đồng kì hạn 12 tháng ở một ngân hàng với lãi suất x%/năm

a) Viết công thức tính số tiền bác Hoa có được sau 12 tháng dưới dạng tích, biết bác Hoa không rút tiền ra khỏi ngân hàng trong 12 tháng đó.

b) Sau kì hạn 12 tháng, tiền lãi của kì hạn đó được cộng vào tiền vốn, rồi bác Hoa tiếp tục đem gửi cho kì hạn 12 tháng tiếp theo. Viết công thức tính tổng số tiền mà bác Hoa nhận được sau khi gửi 24 tháng trên dưới dạng tích, biết trong 24 tháng đó, lãi xuất ngân hàng không thay đổi và bác Hoa không rút tiền ra khỏi ngân hàng.

Phân tích mỗi đa thức sau thành nhân tử:

a) \({\left( {x + 2y} \right)^2} - {\left( {x - y} \right)^2}\)                                           

b) \({\left( {x + 1} \right)^3} + {\left( {x - 1} \right)^3}\)

c) \(9{x^2} - 3x + 2y - 4{y^2}\)                                   

d) \(4{x^2} - 4xy + 2x - y + {y^2}\)

e) \({x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1 - {y^3}\)                                        

g) \({x^3} - 2{{\rm{x}}^2}y + x{y^2} - 4{\rm{x}}\)

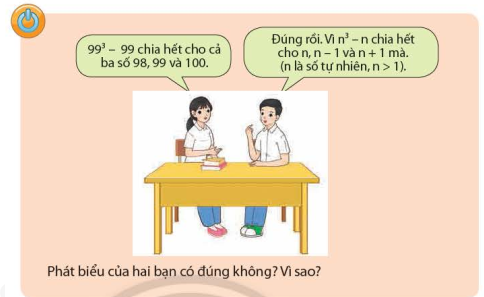
Trả lời câu hỏi nêu trong phần Khởi động: Hưng nhận xét rằng nếu \(n\)là số nguyên dương thì \({n^3} - n\) luôn là tích của ba số tự nhiên liên tiếp. Nhận xét của Hưng đúng hay sai?

Phân tích đa thức sau thành nhân tử:

a)     \(6{x^2}{y^2} + 15{x^2}y - 9x{y^2}\)

b)    \(10xy - 25{x^2} - {y^2}\)

c)     \(27{x^3} - \frac{1}{{64}}\)

d)    \(8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}\)

Phân tích các đa thức sau thành nhân tử:

\(a)xy + xz - 13y - 13z\)

\(b){x^2} + 8x - 9{y^2} + 16\)

\(c){x^3}{y^2} - 2{x^2}y + x\)

\(d){x^2}y - 4{x^2} + 16 - 4y\)

Tính nhanh:

\(a){2022^2} - {22^2}\)

\(b){37^2} + {31^2} - {32^2} + 62.37\)

Phân tích các đa thức sau thành nhân tử:

\(a){x^2} - 4x + 3\)

\(b){x^4} + 4\)

Phân tích các đa thức sau thành nhân tử:

a)     \(2xy + yz - 8x - 4z\)

b)    \(4{x^2} + 4x - 49{y^2} + 1\)

c)     \(9{x^2}{y^4} - 6x{y^3} + {y^2}\)

d)    \({x^3} + x - 8{y^3} - 2y\)

Phân tích mỗi đa thức sau thành nhân tử:

a) \({x^3}\left( {13xy - 5} \right) - {y^3}\left( {5 - 13xy} \right)\)

b) \(8{x^3}yz + 12{x^2}yz + 6xyz + yz\)

Tính giá trị của mỗi biểu thức sau:

a) \(A = {x^2} + xy + \frac{{{y^2}}}{4}\) biết \(x + \frac{y}{2} = 100\)

b) \(B = 25{x^2}z - 10xyz + {y^2}z\) biết \(5x - y =  - 20\) và \(z =  - 5\)

c) \(C = {x^3}yz + 3{x^2}{y^2}z + 3x{y^3}z + {y^4}z\) biết \(x + y =  - 0,5\) và \(yz = 8\)

Chứng minh biểu thức \(B = {x^5} - 15{x^2} - x + 5\) chia hết cho 5 với mọi số nguyên \(x\)

Phân tích các đa thức sau thành nhân tử:

a) \(4{x^3} - 36x\);

b) \(4x{y^2} - 4{x^2}y - {y^3}\);

c) \({x^6} - 64\).

Phân tích mỗi đa thức sau thành nhân tử:

a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\)

b) \({x^2} - x - {y^2} + y\)

c) \({x^3} + 2{x^2} + x - 16x{y^2}\)