Trong các phân số:\(\dfrac{{13}}{{15}};\dfrac{{13}}{4};\dfrac{{ - 1}}{{18}};\dfrac{{11}}{6};\dfrac{7}{{20}};\dfrac{{ - 19}}{{50}}\), gọi A là tập hợp các phân số viết được thành số thập phân hữu hạn và B là tập hợp các phân số viết được thành số thập phân vô hạn tuần hoàn. Liệt kê và viết các phần tử của hai tập hợp đó theo thứ tự từ nhỏ đến lớn.
Các phân số tối giản với mẫu dương mà mẫu chỉ có ước nguyên tố là 2 và 5 đều viết được dưới dạng số thập phân hữu hạn
Các phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 đều viết được dưới dạng số thập phân vô hạn tuần hoàn.
Các phân số trên đã tối giản.
Ta có:
\(\begin{array}{l}15 = 3.5;\\4 = {2^2}\\18 = {2.3^2}\\6 = 2.3\\20 = {2^2}.5\\50 = {2.5^2}\end{array}\)
Như vậy: Tập hợp A gồm các phân số viết được thành số thập phân hữu hạn (mẫu chỉ có ước nguyên tố là 2 và 5) gồm các phần tử: \( - \dfrac{19}{50};\dfrac{7}{20};\dfrac{13}{4}\)
Tập hợp B gồm các phân số viết được thành số thập phân vô hạn tuần hoàn (mẫu có ước nguyên tố khác 2 và 5) gồm các phần tử: \(-\dfrac{1}{{18}};\dfrac{{13}}{{15}};\dfrac{{11}}{6}\)
Vì \( - \dfrac{19}{50}<0<\dfrac{7}{20}<1<\dfrac{13}{4}\) nên \( - \dfrac{19}{50}<\dfrac{7}{20}<\dfrac{13}{4}\)
Vì \(-\dfrac{1}{{18}}<0<\dfrac{{13}}{{15}}<1<\dfrac{{11}}{6}\) nên \(-\dfrac{1}{{18}}<\dfrac{{13}}{{15}}<\dfrac{{11}}{6}\)
Từ đó ta được:
\(\begin{array}{l}A = \left\{ { - \dfrac{{19}}{{50}};\dfrac{7}{{20}};\dfrac{{13}}{4}} \right\}\\B = \left\{ { - \dfrac{1}{{18}};\dfrac{{13}}{{15}};\dfrac{{11}}{6}} \right\}\end{array}\)

Các bài tập cùng chuyên đề
Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn?
\(0,1; - 1,(23);11,2(3); - 6,725\)
Cho bốn phân số: \(\dfrac{17}{80}; \dfrac{611}{125}; \dfrac{133}{91}; \dfrac{9}{8}\)
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết \(\sqrt{2}=1,414213562...\), hãy so sánh phân số tìm được trong câu a) với \(\sqrt{2}\)
Chọn đáp án sai
-
A.
Phân số \(\frac{2}{25}\) được viết dưới dạng số thập phân hữu hạn.
-
B.
Phân số \(\frac{55}{-300}\) được viết dưới dạng số thập phân vô hạn tuần hoàn
-
C.
Phân số \(\frac{63}{77}\) được viết dưới dạng số thập phân hữu hạn
-
D.
Phân số \(\frac{63}{360}\) được viết dưới dạng số thập phân hữu hạn
Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B,C như sau: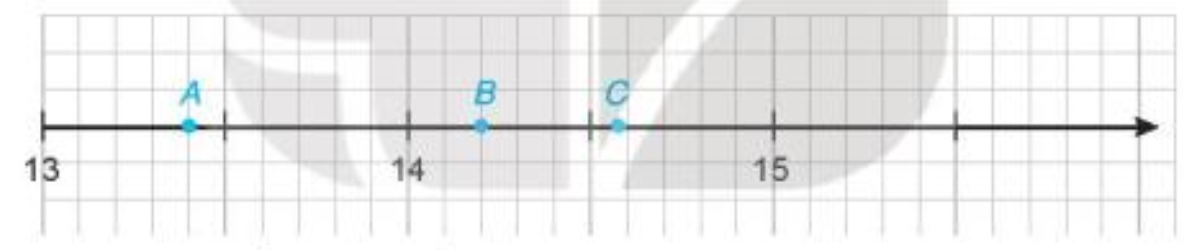
a) Hãy cho biết hai điểm A, B biểu diễn những số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Viết mỗi số sau dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn:
\(\dfrac{1}{3};{\rm{ }}\dfrac{{17}}{6};{\rm{ }}\dfrac{3}{4};{\rm{ }}\dfrac{{ - 14}}{{11}};{\rm{ }}\dfrac{{ - {\rm{ }}4}}{{55}}\).
Cho các số sau \(\frac{4}{6} = 0,66...6;\,\frac{3}{4} = 0,75;\,\frac{{20}}{{15}} = 1,333...3;\,\frac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn?
-
A.
\(\frac{4}{6} = 0,66...6;\,\frac{{20}}{{15}} = 1,333...3\)
-
B.
\(\frac{3}{4} = 0,75;\,\frac{5}{4} = 1,25\)
-
C.
\(\frac{4}{6} = 0,66...6;\,\frac{{3}}{{4}} = 0,75\)
-
D.
\(\frac{4}{6} = 0,666...6;\,\frac{3}{4} = 0,75;\,\frac{{20}}{{15}} = 1,333...3\)







Danh sách bình luận