Cho các biểu thức:
\(\frac{4}{5}x;\left( {\sqrt 2 - 1} \right)xy; - 3x{y^2};\frac{1}{2}{x^2}y;\frac{1}{x}{y^3}; - xy + \sqrt 2 ; - \frac{3}{2}{x^2}y;\frac{{\sqrt x }}{5}.\)
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức, biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
a) Sử dụng khái niệm đơn thức: Đơn thức là biểu thức đại số gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
b) Sử dụng kiến thức về hệ số và phần biến của đơn thức: Phần số trong một đơn thức thu gọn gọi là hệ số; phần còn lại là phần biến của đơn thức đó.
c) Sử dụng khái niệm bậc của đa thức: Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
a) Biểu thức \(\frac{1}{x}{y^3}\) không là đơn thức vì chứa biến x ở mẫu số.
Biểu thức \( - xy + \sqrt 2 \) không là đơn thức vì chứa phép cộng với các biến.
Biểu thức \(\frac{{\sqrt x }}{5}\) không là đơn thức vì chứa biến x ở trong căn bậc hai.
Các biểu thức còn lại đều là đơn thức.
b) Các đơn thức là: \(\frac{4}{5}x\) ; \((\sqrt 2 - 1)xy\) ; \( - 3x{y^2}\) ; \(\frac{1}{2}{x^2}y\) ; \( - \frac{3}{2}{x^2}y\) .
- Đơn thức \(\frac{4}{5}x\) có hệ số là \(\frac{4}{5}\) và phần biến là \(x\) .
- Đơn thức \((\sqrt 2 - 1)xy\) có hệ số là \(\sqrt 2 - 1\) và phần biến là \(xy\) .
- Đơn thức \( - 3x{y^2}\) có hệ số là \( - 3\) và phần biến là \(x{y^2}\) .
- Đơn thức \(\frac{1}{2}{x^2}y\) có hệ số là \(\frac{1}{2}\) và phần biến là \({x^2}y\) .
- Đơn thức \( - \frac{3}{2}{x^2}y\) có hệ số là \( - \frac{3}{2}\) và phần biến là \({x^2}y\) .
c) Đa thức tổng của các đơn thức trên là:
\(\begin{array}{l}\frac{4}{5}x + \left( {\sqrt 2 - 1} \right)xy + \left( { - 3x{y^2}} \right) + \frac{1}{2}{x^2}y + \left( { - \frac{3}{2}{x^2}y} \right)\\ = \frac{4}{5}x + \left( {\sqrt 2 - 1} \right)xy - 3x{y^2} - {x^2}y.\end{array}\)
Hạng tử có bậc cao nhất là \( - 3x{y^2}\) và \( - {x^2}y\) có bậc là \(1 + 2 = 2 + 1 = 3\) . Vậy bậc của đa thức \(\frac{4}{5}x + \left( {\sqrt 2 - 1} \right)xy - 3x{y^2} - {x^2}y\) là 3.

Các bài tập cùng chuyên đề
Một bức tường hình thang có cửa sổ hình tròn với các kích thước như hình 1 (tính bằng m).
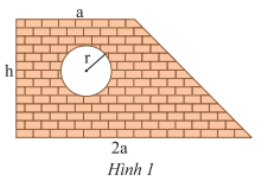
a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ).
b) Tính giá trị diện tích trên khi \(a = 2\)m; \(h = 3m\), \(r = 0,5\)m (lấy \(\pi = 3,14\); làm tròn kết quả đến hàng trăm).
Cho các biểu thức sau:
\(ab - \pi {r^2}\); \(\dfrac{{4\pi {r^3}}}{3}\); \(\dfrac{p}{{2\pi }}\); \(x - \dfrac{1}{y}\); \(0\); \(\dfrac{1}{{\sqrt 2 }}\); \({x^3} - x + 1\).
Trong các biểu thức trên, hãy chỉ ra:
a) Các đơn thức;
b) Các đa thức và số hạng tử của chúng
Một số biểu thức được phân chia thành các nhóm như dưới đây:

a) Các biểu thức ở nhóm A có đặc điểm gì phân biệt với các biểu thức ở nhóm B và nhóm C?
b) Các biểu thức ở nhóm A và nhóm B có đặc điểm gì chung, phân biệt với các biểu thức ở nhóm C?
Chỉ ra các đơn thức, đa thức trong các biểu thức sau:
\( - 3\); \(2z\); \(\dfrac{1}{3}xy + 1\); \( - 10{x^2}yz\); \(\dfrac{4}{{xy}}\); \(5x - \dfrac{z}{2}\); \(1 + \dfrac{1}{y}\)
Tính giá trị của đa thức \(P = x{y^2}z - 2{x^2}y{z^2} + 3yz + 1\) khi \(x = 1\); \(y = - 1\); \(z = 2\)
a) Trong các biểu thức sau, biểu thức nào là đơn thức:
\(\dfrac{1}{5}x{y^2}{z^3};3 - 2{{\rm{x}}^3}{y^2}z; - \dfrac{3}{2}{x^4}{\rm{yx}}{{\rm{z}}^2};\dfrac{1}{2}{x^2}\left( {{y^3} - {z^3}} \right)\)
b) Trong những biểu thức sau, biểu thức nào là đa thức:
\(2 - x + y; \dfrac{{x - y}}{{x{y^2}}};- 5{{\rm{x}}^2}y{z^3} + \dfrac{1}{3}x{y^2}z + x + 1; \dfrac{1}{x} + 2y - 3{\rm{z}}\)
Cho hai đa thức: \(A = 4{{\rm{x}}^6} - 2{{\rm{x}}^2}{y^3} - 5{\rm{x}}y + 2;B = 3{{\rm{x}}^2}{y^3} + 5{\rm{x}}y - 7\)
a) Tính giá trị của mỗi đa thức A, B tại x = -1; y = 1
b) Tính A + B; A - B
Cho các biểu thức đại số:
\(11\); \(3{x^2}y\); \(7x\); \(x - 2y\); \(\frac{{ - 3}}{5}x{y^2}{z^2}\);
\(4{x^2} + y\); \(28{x^2}\left( { - \frac{1}{2}} \right){y^3}x\); \(6\left( {x + {y^2}} \right)\); \(9y - 1\)
Hãy sắp xếp chúng thành 2 nhóm:
- Nhóm 1: Các biểu thức có chứa phép cộng và phép trừ
- Nhóm 2: Các biểu thức còn lại
Thu gọn và tìm bậc của mỗi đa thức sau:
a) \(6x - 3y - 4x - y + 3x - 1\);
b) \(3{x^2}y + 2x{y^2} - 3x{y^2} - 2{x^2}y\);
c) \({x^2}yz - \frac{1}{2}zy{x^2} + \frac{1}{2}yx{z^2}\);
d) \( - 2xyx + 6y{x^2}y + 5{x^2}y - 4{x^2}{y^2} - 5x{y^2}x\).
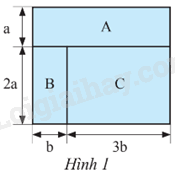
Cho ba hình chữ nhật A, B, C với các kích thước như Hình 1. Tính diện tích của mỗi hình chữ nhật này và tổng diện tích của chúng.
a) Trong các biểu thức sau, biểu thức nào là đơn thức?
\(\frac{{\sqrt 2 }}{{11}}x\); \( - 3x + {y^4}\); \( - 3x{y^4}z\); \(\frac{{ - 1}}{{321}}{x^3}{y^5} + 7\)
b) Trong các biểu thức sau, biểu thức nào là đa thức?
\(\frac{{ - 13}}{{21}}{x^3}{y^2} + 9x{y^6} - 8\); \(x + y\); \(xyz + \sqrt 2 \); \(\frac{{x - 5z}}{{{x^2} + {z^2} + 1}}\)
Kết quả của phép cộng hai đơn thức \(2x{y^2}z\) và \( - 0,2{x^2}yz\) là
A. Một đơn thức.
B. Không xác định.
C. Một đa thức.
D. Một số.
Thu gọn biểu thức:
a) \( 65x^9y^5 : (-13x^4y^4) \)
b) \( x(x - y) - y(y^2 - x) \)
c) \( (x - y)(x^2 + y^2) - (x^4y - xy^4) : xy \)
Trong các biểu thức sau, biểu thức nào là đơn thức bậc 5?
-
A.
\({x^5}y + 1\)
-
B.
\({x^2} + {y^3}\)
-
C.
\({x^2}{y^5}\)
-
D.
\(x{y^2}zx\)







Danh sách bình luận