Phân tích mỗi đa thức sau thành nhân tử:
a) \(25{x^2} - \frac{1}{4}\)
b) \(36{x^2} + 12xy + {y^2}\)
c) \(\frac{{{x^3}}}{2} + 4\)
d) \(27{y^3} + 27{y^2} + 9y + 1\)
Ta có thể phân tích đa thức thành nhân tử bằng cách vận dụng trực tiếp hằng đẳng thức hoặc bằng cách vận dụng hằng đẳng thức thông qua nhóm số hạng và đặt nhân tử chung.
a) \(25{x^2} - \frac{1}{4} = {\left( {5x} \right)^2} - {\left( {\frac{1}{2}} \right)^2} = \left( {5x + \frac{1}{2}} \right)\left( {5x - \frac{1}{2}} \right)\)
b) \(36{x^2} + 12xy + {y^2} = {\left( {6x} \right)^2} + 2.6x.y + {y^2} = {\left( {6x + y} \right)^2}\)
c) \(\frac{{{x^3}}}{2} + 4 = \frac{1}{2}\left( {{x^3} + 8} \right) = \frac{1}{2}\left( {{x^3} + {2^3}} \right) = \frac{1}{2}\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)\)
d) \(27{y^3} + 27{y^2} + 9y + 1 = {\left( {3y} \right)^3} + 3.{\left( {3y} \right)^2}.1 + 3.3y{.1^3} + {1^3} = {\left( {3y + 1} \right)^3}\)
Các bài tập cùng chuyên đề
Phân tích các đa thức sau thành nhân tử
a) \({\left( {x + 1} \right)^2} - {y^2}\)
b) \({x^3} + 3{x^2} + 3x + 1\)
c) \(8{x^3} - 12{x^2} + 6x - 1\)
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
a) \(4{x^2} - 9 \);
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2}\)
Phân tích các đa thức sau thành nhân tử:
a) \(9{x^2} - 16\)
b) \(4{x^2} - 12xy + 9{y^2}\)
c) \({t^3} - 8\)
d) \(2a{x^3}{y^3} + 2a\)
Phân tích các đa thức sau thành nhân tử:
a) \(4{x^2} - 1\)
b) \({\left( {x + 2} \right)^2} - 9\)
c) \({\left( {a + b} \right)^2} - {\left( {a - 2b} \right)^2}\)
Phân tích các đa thức sau thành nhân tử:
a) \(4{a^2} + 4a + 1\)
b) \( - 3{x^2} + 6xy - 3{y^2}\)
c) \({\left( {x + y} \right)^2} - 2\left( {x + y} \right)z + {z^2}\)
Cho \(y > 0\). Tìm độ dài cạnh của hình vuông có diện tích bằng \(49{y^2} + 28y + 4\)
Khi phân tích đa thức \(R = 4{x^2} - 4xy + {y^2}\) thành nhân tử thì được:
A. \(R = {(x + 2y)^2}\)
B. \(R = {(x - 2y)^2}\)
C. \(R = {(2x + y)^2}\)
D. \(R = {(2x - y)^2}\)
Khi phân tích đa thức \(S = {x^6} - 8\) thành nhân tử thì được:
A. \(S = \left( {{x^2} + 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)
B. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)
C. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)
D. \(S = \left( {x - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)
Viết mỗi đa thức sau dưới dạng tích của hai đa thức:
\(a){x^2} - {y^2}\) \(b){x^3} - {y^3}\) \(c){x^3} + {y^3}\)
Phân tích mỗi đa thức sau thành nhân tử:
\(a){\left( {x + 2y} \right)^2} - {\left( {2{\rm{x}} - y} \right)^2}\)
\(b)125 + {y^3}\)
\(c)27{{\rm{x}}^3} - {y^3}\)
Phân tích mỗi đa thức sau thành nhân tử:
\(a)4{{\rm{x}}^2} - 12{\rm{x}}y + 9{y^2}\)
\(b){x^3} + 9{{\rm{x}}^2} + 27{\rm{x}} + 27\)
\(c)8{y^3} - 12{y^2} + 6y - 1\)
\(d){\left( {2{\rm{x}} + y} \right)^2} - 4{y^2}\)
\(e)27{y^3} + 8\)
\(g)64 - 125{{\rm{x}}^3}\)
Dùng hằng đẳng thức “Bình phương của một tổng”, ta có thể phân tích đa thức \({x^2} + 4x + 4\) thành nhân tử như sau:
\({x^2} + 4x + 4 = {\left( {x + 2} \right)^2} = \left( {x + 2} \right).\left( {x + 2} \right)\).
a) Hãy dùng hằng đẳng thức “Hiệu hai bình phương” để phân tích đa thức \({x^2} - 9\) thành nhân tử.
b) Hãy dùng một hằng đẳng thức thích hợp để phân tích đa thức \(8 - {x^3}\) thành nhân tử.
Phân tích các đa thức sau thành nhân tử:
a) \({\left( {x - y} \right)^2} - 16{y^2}\)
b) \(27{x^2} - \frac{1}{8}{y^3}\)
Độ cao \(h\)(feet) của một vật so với mặt đất sau thời gian \(t\) (giây) kể từ lúc rơi được cho bởi: \(h = 25 - 16{t^2}\)
a) Tìm độ cao của vật so với mặt đất sau 1 giây kể từ lúc rơi.
b) Một học sinh đã viết lại \(h = {\left( {5 - 4{t^2}} \right)^2}\). Học sinh này viết đúng hay sai?
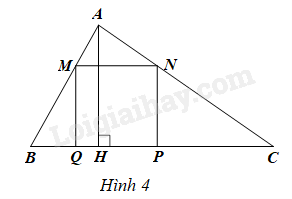
Cho tam giác \(ABC\) có cạnh \(BC = 2x\left( {dm} \right)\), đường cao \(AH = x\left( {dm} \right)\) với \(x > 0\) và hình vuông \(MNPQ\) có cạnh \(MN = y\left( {dm} \right)\) với \(y > 0\) (Hình 4).
a) Viết công thức tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\) dưới dạng tích.
b) Tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\), biết \(x - y = 2\) và \(x + y = 10\)
Phân tích đa các đa thức sau thành nhân tử:
a) \(100 - {x^2}\);
b) \(4{x^2} - {y^2}\);
c) \({\left( {x + y} \right)^2} - \frac{1}{4}{y^2}\);
d) \({\left( {x - y} \right)^2} - {\left( {y - z} \right)^2}\);
e) \({x^2} - {\left( {1 + 2x} \right)^2}\);
g) \({x^4} - 16\).
Phân tích các đa thức sau thành nhân tử:
a) \({a^2} + 12a + 36\);
b) \( - 9 + 6a - {a^2}\);
c) \(2{a^2} + 8{b^2} - 8ab\);
d) \(16{a^2} + 8a{b^2} + {b^4}\).
Phân tích các đa thức sau thành nhân tử:
a) \({x^3} - 1000\);
b) \(8{x^3} + {\left( {x - y} \right)^3}\);
c) \({\left( {x - 1} \right)^3} - 27\);
d) \({x^6} + {y^9}\).
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính S khi \(x = 102m,y = 2m\).
Phân tích đa thức sau thành nhân tử: \(x^2-6x-y^2+9\)
Phân tích đa thức \(3{x^2} - 6xy + 3{y^2} - 12{z^2}\) thành nhân tử ta được
Phân tích mỗi đa thức sau thành nhân tử:
a) \(8{x^3}yz + 12{x^2}yz + 6xyz + yz;\;\;\;\)
b) \(81{x^4}\left( {{z^2} - {y^2}} \right) - {z^2} + {y^2};\)
c) \(\frac{{{x^3}}}{8} - \frac{{{y^3}}}{{27}} + \frac{x}{2} - \frac{y}{3};\;\)
d) \({x^6} + {x^4} + {x^2}{y^2} + {y^4} - {y^6}\)
Cho đa thức: \(P = {x^2} - {y^2} + 6{\rm{x}} + 9\)
a) Phân tích đa thức P thành nhân tử
b) Sử dụng kết quả của câu a để tìm thương của phép chia đa thức P cho x+y+3
Giải các phương trình sau:
a) \(5\left( {x - 3} \right) + 5 = 4x + 1\)
b) \({x^3} - 1 + \left( {1 - x} \right)\left( {x - 5} \right) = 0\)
