Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4)
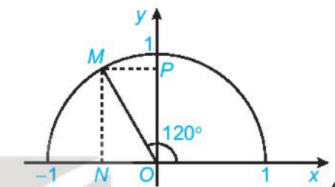
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {120^o},\;\sin {120^o}\)
Từ đó suy ra \(\;\tan {120^o} = \dfrac{{\sin {{120}^o}}}{{\cos {{120}^o}}},\;\;\cot {120^o} = \dfrac{{\cos {{120}^o}}}{{\sin {{120}^o}}}.\)
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
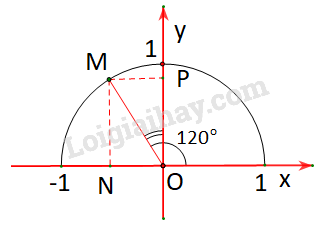
Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))

Các bài tập cùng chuyên đề
a) Tính \(\cos {80^o}43'51'';\tan {147^o}12'25'';\cot {99^o}9'19''.\)
b) Tìm \(\alpha \;({0^o} \le \alpha \le {180^o}),\) biết \(\cos \alpha = - 0,723.\)
Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:
a) Tính \(\sin {168^o}45'33'';\cos {17^o}22'35'';\tan {156^o}26'39'';\cot {56^o}36'42''.\)
b) Tìm \(\alpha \;({0^o} \le \alpha \le {180^o}),\)trong các trường hợp sau:
i) \(\sin \alpha = 0,862.\)
ii) \(\cos \alpha = - 0,567.\)
iii) \(\tan \alpha = 0,334.\)
Dùng máy tính cầm tay, tính:
a) \(\sin 130^\circ 12'24''\)
b) \(\cos 144^\circ 35'12''\)
c) \(\tan 152^\circ 35'44''\)
Dùng máy tính cầm tay, tìm x biết:
a) \(\cos x = - 0,234\)
b) \(\sin x = 0,812\)
c) \(\cot x = - 0,333\)
Bất đẳng thức nào sau đây là bất đẳng thức đúng?
A. \(\sin 90^\circ < \sin 150^\circ \)
B. \(\sin 90^\circ 15' < \sin 90^\circ 30'\)
C. \(\sin 90^\circ 30' > \cos 100^\circ \)
D. \(\cos 150^\circ > \cos 120^\circ \)







Danh sách bình luận