Giải bài toán ở hoạt động khởi động (Trang 11)

Một toà nhà cao tầng có hai tầng hầm. Tầng hầm B1 có chiều cao 2,7 m. Tầng hầm B2 có chiều cao bằng \(\frac{4}{3}\) tầng hầm B1. Tính chiều cao tầng hầm của toà nhà so với mặt đất.

Giả sử một khinh khí cầu bay lên từ mặt đất theo chiều thẳng đứng với vận tốc 0,8 m/s trong 50 giây. Sau đó nó giảm dần độ cao với vận tốc \(\dfrac{5}{9}\) m/s. Hỏi sau 27 giây từ khi hạ độ cao, khinh khí cầu cách mặt đất bao nhiêu mét?

Tính một cách hợp lí: \(\frac{7}{6}.3\frac{1}{4} + \frac{7}{6}.( - 0,25).\)

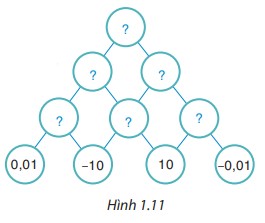
Thay mỗi dấu “?” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.11, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.

Nhiệt độ đo được vào một buổi tối mùa đông tại Sa Pa là -1,8 °C. Nhiệt độ buổi chiều hôm đó bằng \(\frac{2}{3}\) nhiệt độ buổi tối. Hỏi nhiệt độ ở Sa Pa buổi chiều hôm đó là bao nhiêu độ C?

Tính:

a)\(\left( { - 3,5} \right).\left( {1\frac{3}{5}} \right);\)                   b) \(\frac{{ - 5}}{9}.\left( { - 2\frac{1}{2}} \right).\)

Cho biểu thức M = \(\frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\). Hãy tính giá trị của M theo 2 cách:

a) Thực hiện tính nhân rồi cộng 2 kết quả

b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng

Tính:

a)\(A = \frac{5}{{11}}.\left( {\frac{{ - 3}}{{23}}} \right).\frac{{11}}{5}.\left( { - 4,6} \right);\)        b) \(B = \left( {\frac{{ - 7}}{9}} \right).\frac{{13}}{{25}} - \frac{{13}}{{25}}.\frac{2}{9}\)

Đường kính của Sao Kim bằng \(\frac{6}{{25}}\) đường kính của Sao Thiên Vương. Đường kính của Sao Thiên Vương bằng \(\frac{5}{{14}}\) đường kính của Sao Mộc.

a) Đường kính của Sao Kim bằng bao nhiêu phần đường kính của Sao Mộc?

b) Biết rằng đường kính của Sao Mộc khoảng 140 000 km, tính đường kính của Sao Kim.

(Theo: https://vi.wikipedia.org/wiki/Hệ Mặt Trời)

Nêu tính chất của phép nhân các số nguyên.

Một trường trung học cơ sở có các lớp 7A, 7B, 7C, 7D, 7E; mỗi lớp đều có 40 học sinh. Sau khi sơ kết Học kì I, số học sinh ở mức Tốt của mỗi lớp đó được thể hiện qua biểu đồ cột ở Hình 5 .

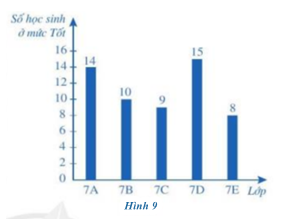
a) Lớp nào có số học sinh ở mức Tốt ít hơn một phần tư số học sinh của cả lớp?

b) Lớp nào có số học sinh ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp?

c) Lớp nào có tỉ lệ học sinh ở mức Tốt cao nhất, thấp nhất?

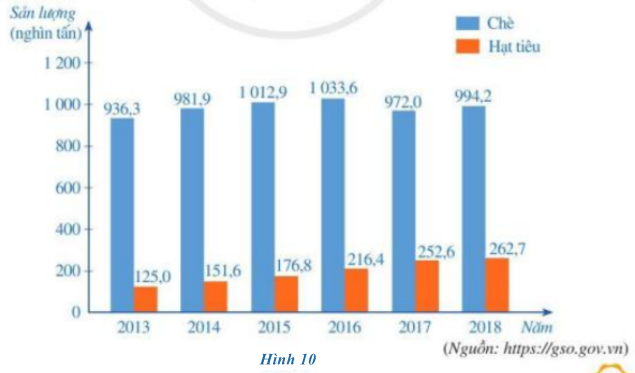
Sản lượng chè và hạt tiêu xuất khẩu của Việt Nam qua một số năm được biểu diễn trong biểu đồ cột kép ở Hình 6 .

a) Những năm nào sản lượng chè xuất khẩu trên 1 triệu tấn? Sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn?

b) Năm nào Việt Nam có sản lượng chè xuất khẩu lớn nhất? Sản lượng hạt tiêu xuất khẩu lớn nhất?

c) Tính tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018. (làm tròn kết quả đến hàng đơn vị)

Với bài tập: Tính tổng \(A =  - 5,2.72 + 69,1 + 5,2.\left( { - 28} \right) + \left( { - 1,1} \right)\). Hai bạn Vuông và Tròn đã làm như sau:

a) Em hãy giải thích cách làm của mỗi bạn.

b) Theo em, nên làm theo cách nào?

Tính bằng cách hợp lí giá trị của các biểu thức:

a)\(A = \left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( { - \dfrac{4}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\)

b)\(B = 2022,2021 \cdot 1954,1945 + 2022,2021 \cdot \left( { - 1954,1945} \right)\)

Chim ruồi “khổng lồ” Nam Mỹ (Giant hummingbird of South America) là loại chim ruồi to nhất trên thế giới. Nó dài gấp \(4\dfrac{1}{8}\) lần chim ruồi ong (bee humminbird).

Nếu độ dài của chim ruồi ong là 5,5 cm thì độ dài của chim ruồi “khổng lồ” Nam Mỹ là bao nhiêu?

Tính một cách hợp lí

\(\frac{{17}}{{19}}.\left( { - 0,5} \right).\frac{{ - 38}}{{17}}.\)

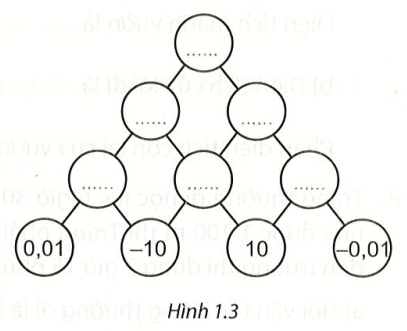
Thay mỗi dấu “...” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.3, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.

Một cửa hàng điện máy nhập về 100 chiếc máy tính xách tay với giá 8 triệu đồng một chiếc. Sau khi đã bán được 70 chiếc với tiền lãi bằng 30% giá vốn, số máy còn lại được bán với mức giá bằng 65% giá bán trước đó. Hỏi sau khi bán hết lô hàng thì cửa hàng lời hay lỗ bao nhiêu tiền?

Kết quả của phép tính \( - \,\,0,35\,\,.\,\,\frac{2}{7} = ?\)

Cho hai số hữu tỉ x = \(\frac{a}{b}\); y = \(\frac{c}{d}\) (với a, b, c, d \( \in \mathbb{Z}\); b, d ≠ 0). Vậy x . y = ?

Thực hiện phép tính (tính hợp lý nếu có thể):

\(1,2  .  \frac{15}{4}+\frac{16}{7} . \frac{ −85}{8}−1,2  .  5\frac{3}{4}−\frac{16}{7} . \frac{ −71}{8}\)

Thực hiện phép tính (Tính hợp lí nếu có thể):

\(\left( { - \frac{5}{9}} \right).\frac{3}{{11}} + \left( { - \frac{{13}}{{18}}} \right).\frac{3}{{11}}\)

Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

\(\frac{1}{{2023}}.\frac{{ - 7}}{9} + \frac{{2022}}{{2023}}.\frac{{ - 7}}{9} + \frac{7}{9}\)