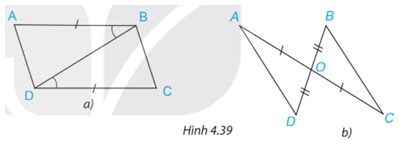
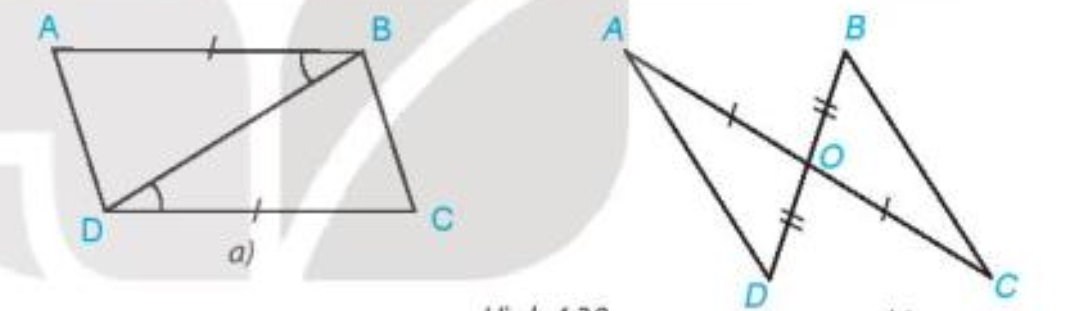
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)

Các bài tập cùng chuyên đề
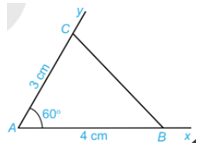
Vẽ \(\widehat {xAy}\) = 60°. Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. Nối điểm B với điểm C ta được tam giác ABC (H.4.27)
Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.
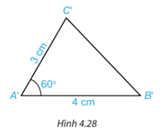
Vẽ thêm tam giác A’B’C’ với \(\widehat {B'A'C'}\)= 60°, A’B’ = 4 cm và A'C'= 3 cm (H.4.28).
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và ABC.
- Hai tam giác ABC và ABC có bằng nhau không?
- Độ dài các cạnh AB và AB của hai tam giác em vừa vẽ có bằng các cạnh AB và AB của hai tam giác các bạn khác về không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
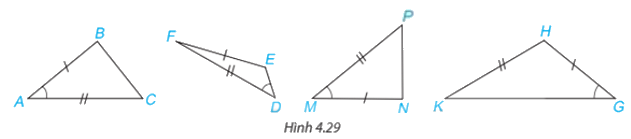
Trong Hình 4.29, hai tam giác nào bằng nhau?
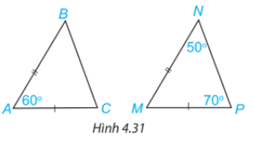
Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?
Cho Hình 4.32, biết \(\widehat {OAB} = \widehat {ODC},OA = OD\) và \(AB = CD\).
Chứng minh rằng:
a) \(AC = DB\);
b) \(\Delta OAC = \Delta ODB\).
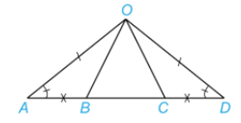
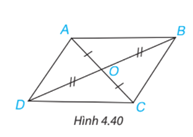
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng \(\Delta \)DAB = \(\Delta \)BCD.
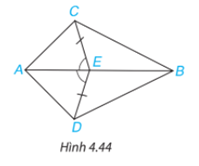
Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:
a) \(\Delta AEC = \Delta AED\)
b) \(\Delta ABC = \Delta ABD.\)
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) \(\Delta \)OAN = \(\Delta \)OBM;
b) \(\Delta \)AMN = \(\Delta \)BNM.
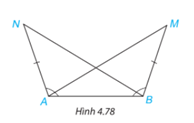
Trong Hình 4.78, ta có AN = BM, \(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng \(\widehat {BAM} = \widehat {ABN}\).
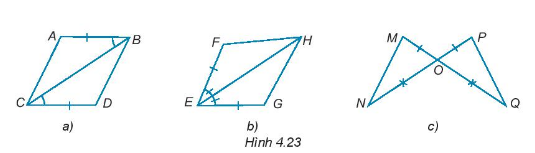
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Cho 2 tam giác ABC và DEF bất kì, thoả mãn AB = FE, BC = DF, \(\widehat {ABC} = \widehat {DFE}\). Những câu nào dưới đây đúng?
a) \(\Delta ABC = \Delta DFE\)
b) \(\Delta BAC = \Delta EFD\)
c) \(\Delta CBA = \Delta EFD\)
d) \(\Delta ABC = \Delta EFD\)
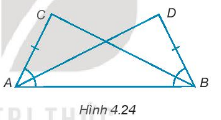
Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và \(\widehat {DBA} = \widehat {CAB}\). Chứng minh rằng AD = BC.
Hai tam giác ABC và MNP bằng nhau khi và chỉ khi điều nào dưới đây xảy ra?
A. AB = MN,AC = MP, \(\widehat A = \widehat M\)
B. AB = MN, AC = MP, \(\widehat B = \widehat N\)
C. AB = MP, AC = MN,\(\widehat A = \widehat M\)
D. AB = AC, MN = MP,\(\widehat A = \widehat M.\)
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
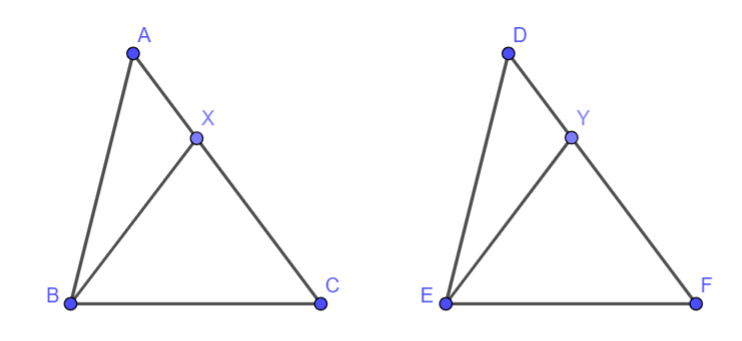
Cho tam giác ABC bằng tam giác DEF. Trên các cạnh AC và DF lấy các điểm X, Y sao cho AX = DY . Chứng minh rằng \(\widehat {BXC} = \widehat {EYF}\)
Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, \(\widehat A = \widehat D = {60^o}\), BC = 6cm, \(\widehat {ABC} = {45^o}\). Hãy tính độ dài cạnh EF và số đo các góc C, E, F.
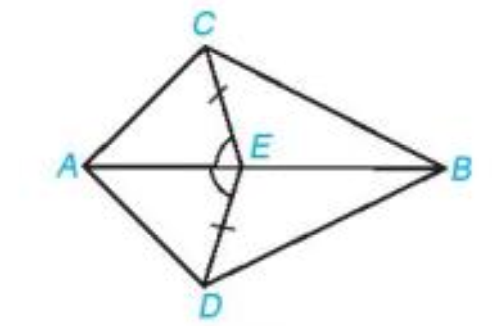
Cho năm điểm A, B, C, D, E thỏa mãn EC = ED và \(\widehat {AEC} = \widehat {AED}\) như hình vẽ dưới đây. Chứng minh rằng:
a) \(\Delta AEC = \Delta AED\)
b) \(\Delta ABC = \Delta ABD\)
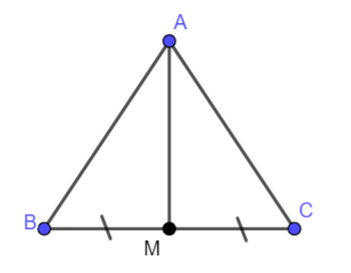
Cho tam giác ABC cân tại A và M là trung điểm của BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Cho góc xOy. Trên tia Ox lấy hai điểm A, M, trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.Chứng minh rằng:
a) \(\Delta OAN = \Delta OBM\)
b) \(\Delta AMN = \Delta BNM\)

Trong hình sau, ta có AM = BN, \(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng \(\widehat {BAM} = \widehat {ABN}\).
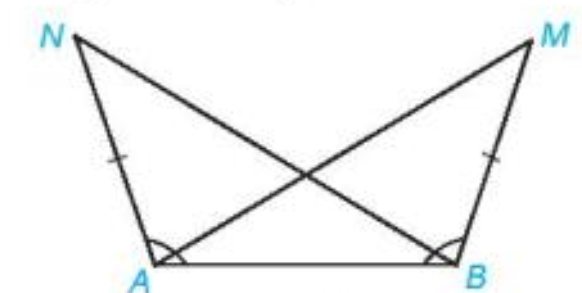
Cho tam giác ABC như trong Hình 8a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có \(\widehat {B'} = \widehat B\), B’A’ = BA, B’C’ = BC theo các bước:
- Vẽ \(\widehat {xB'y} = \widehat {ABC}\)
- Trên tia B’x lấy đoạn B’A’= BA.
- Trên tia B’y lấy đoạn B’C’ = BC.
-Vẽ đoạn A’C’, ta được tam giác A’B’C’(Hình 8b)
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
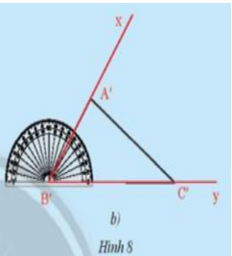
Nêu thêm điều kiện để hai tam giác trong mỗi hình bên (Hình 15a,b) bằng nhau theo trường hợp cạnh – góc – cạnh.
Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của \(\widehat {GFH}\). Chứng minh rằng hai tam giác FIG và FIH bằng nhau.
Cho hình vẽ

Hai tam giác trên bằng nhau theo trường hợp
-
A.
Cạnh – góc – góc;
-
B.
Cạnh – góc – cạnh;
-
C.
Góc – cạnh – góc;
-
D.
Cả A, B, C đều đúng.
Hai chiếc compa ở Hình 45 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, AC = A’C’, \(\widehat A = \widehat {A'}\).

Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.
Chứng minh định lí: “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” (trang 74) thông qua việc giải bài tập sua đây:
Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại D. Điểm E thuộc cạnh AC thỏa mãn AE = AB. Chứng minh:
a) \(\Delta ABD = \Delta AED\); b) \(\widehat B > \widehat C\).
Cho \(\Delta ABC = \Delta MNP\). Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh:
a) AD = MQ;
b) DE = QR.
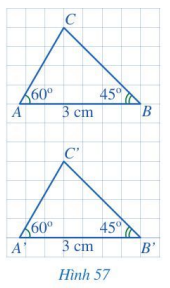
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?







Danh sách bình luận