Cho ba tia Ou, Ov, Owvới số đo của các góc hình học uOv và vOw lần lượt là \({30^ \circ }\) và \({45^ \circ }\)
a) Xác định số đo của ba góc lượng giác \((Ou,Ov)\) ,\((Ov,Ow\) và \((Ou,Ow)\) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ\((Ou,Ov)\) + sđ\((Ov,Ow\) = sđ \((Ou,Ow)\) + k\({.360^ \circ }\)
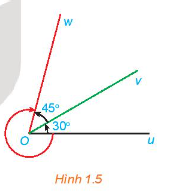
Xác định các tia đầu, tia cuối và chiều quay để tìm được số đo của các góc lượng giác.
a) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là
sđ\((Ou,Ov) = {30^ \circ } + n{.360^ \circ }\)
- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là
sđ \((Ov,Ow) = {45^ \circ } + m{.360^ \circ }\)
- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là
sđ \((Ou,Ow) = {75^ \circ } + k{.360^ \circ }\)
b) Với các góc lượng giác ở câu a, ta có:
\(sđ(Ou,Ov) +sđ (Ov,Ow)\)
\( = {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)
\(= {75^ \circ } + (n+m){.360^ \circ } \)
\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)
với k = n + m
Các bài tập cùng chuyên đề
Cho một góc lượng giác $(O x, O u)$ có số đo $240^{\circ}$ và một góc lượng giác $(O x, O v)$ có số đo $-270^{\circ}$. Tính số đo của các góc lượng giác $(O u, O v)$.
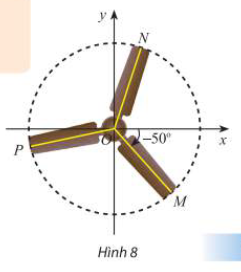
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).
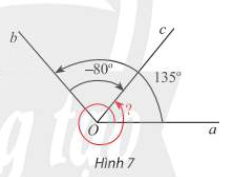
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là \(\frac{\pi }{4}\). Số đo của các góc lượng giác nào sau đây có cùng tia đầu là \(Ou\) và tia cuối là \(Ov\)?
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
