Tại một hồ trong công viên nước, một con cá heo nhảy lên khỏi mặt nước với vận tốc ban đầu của cú nhảy là 20 ft/giây (1 ft = 30,48 cm) (Hình 1.12).
Độ cao \(h\) (ft) của cá heo so với mặt nước sau thời gian \(t\) giây kể từ lúc nhảy được tính bởi \(h = 20t - 16{t^2}\).

a) Chứng minh rằng \(h = 4t\left( {5 - 4t} \right)\).
b) Tính độ cao của cá heo so với mặt nước sau 0,5s kể từ lúc nhảy.
Áp dụng phương pháp phân tích đa thức thành nhân tử bằng cách tìm nhân tử chung.
Tính độ cao của cá heo bằng cách thay \(t = 0,5\) vào công thức tính độ cao.
a) Ta có:
\(h = 20t - 16{t^2} = 4t\left( {5 - 4t} \right)\)
b) Thay \(t = 0,5\) vào công thức tính độ cao \(h = 4t\left( {5 - 4t} \right)\):
\(h = 4.0,5\left( {5 - 4.0,5} \right) = 6\)

Các bài tập cùng chuyên đề
Hãy viết đa thức \({x^2} - 2xy\) thành tích của các đa thức, khác đa thức là số.
Phân tích các đa thức sau thành nhân tử:
a) \(6{y^3} + 2y\)
b) \(4\left( {x - y} \right) - 3x\left( {x - y} \right)\)
Giải bài toán mở đầu bằng cách phân tích \(2{x^2} + x\) thành nhân tử.
Tìm x biết:
a) \({x^2} - 4x = 0\)
b) \(2{x^3} - 2x = 0\)
Phân tích các đa thức sau thành nhân tử:
a) \(P = 6x - 2{x^3}\)
b) \(Q = 5{x^3} - 15{x^2}y\)
c) \(R = 3{x^3}{y^3} - 6x{y^3}z + xy\)
Phân tích các đa thức sau thành nhân tử:
a) \({x^3} + 4x\)
b) \(6ab - 9a{b^2}\)
c) \(2a\left( {x - 1} \right) + 3b\left( {1 - x} \right)\)
d) \({\left( {x - y} \right)^2} - x\left( {y - x} \right)\)
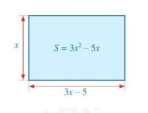
Làm thế nào để biến đổi được đa thức \(3{{\rm{x}}^2} - 5{\rm{x}}\) dưới dạng tích của hai đa thức?
Viết đa thức \(3{{\rm{x}}^2} - 5{\rm{x}}\) thành tích của hai đa thức bậc nhất?
Phân tích mỗi đa thức sau thành nhân tử:
\(a)3{{\rm{x}}^2} - 6{\rm{x}}y + 3{y^2} - 5{\rm{x}} + 5y\)
\(b)2{{\rm{x}}^2}y + 4{\rm{x}}{y^2} + 2{y^3} - 8y\)
Chứng tỏ rằng:
\(a)M = {32^{2023}} - {32^{2021}}\) chia hết cho 31
b) \(N = {7^6} + {2.7^3} + {8^{2022}} + 1\) chia hết cho 8
Cho đa thức \(P = 3{x^2} + 6x\). Ta nhận thấy các biểu thức \(3{x^2}\) và \(6x\) trong đa thức \(P\) cùng chia hết cho \(x\). Ta gọi \(x\) là một nhân tử chung của \(3{x^2}\)và \(6x\).
- \(3x\) có phải một nhân tử chung của \(3{x^2}\) và \(6x\)không?
- Hãy cho biết tính chất nào của phép nhân các số đã được sử dụng khi viết
\(3{x^2} + 6x = 3x.x + 3x.2 = 3x\left( {x + 2} \right)\).
Phân tích các đa thức sau thành nhân tử:
a) \(6{x^3} + 24{x^2}\)
b) \(10x\left( {x - y} \right) - 15y\left( {y - x} \right)\)
Tính nhanh \(35.71,2 + 350.2,88.\)
Số lượng sản phẩm N của một công ty bán ra vào ngày phát hành sản phẩm đó được cho bởi:
\(N = 2{x^3} + 4{x^2} + 2x\) (nghìn)
Trong đó \(x\) là số giờ kể từ thời điểm phát hành.
a) Hỏi công ty bán ra được bao nhiêu sản phẩn sau 1 giờ phát hành?
b) Phân tích đa thức N thành nhân tử. Từ đó tính được số sản phẩm công ty bán ra sau 9 giờ phát hành.
Phân tích các đa thức sau thành nhân tử:
a) \(3{x^2} + 6xy\);
b) \(5\left( {y - 3} \right) - x\left( {3 - y} \right)\);
c) \(2{x^3} - 6{x^2}\);
d) \({x^4}{y^2} + x{y^3}\);
e) \(xy - 2xyz + {x^2}y\);
g) \({\left( {x + y} \right)^3} - x{\left( {x + y} \right)^2}\).
Phân tích đa thức \({x^2}\left( {x + 1} \right) - x\left( {x + 1} \right)\) thành nhân tử, ta nhận được
A. x
B. \(x\left( {x + 1} \right)\)
C. \(x\left( {x - 1} \right)\left( {x + 1} \right)\)
D. \(x{\left( {x + 1} \right)^2}\)
Phân tích đa thức \({\left( {x - 4} \right)^2} + \left( {x - 4} \right)\) thành nhân tử, ta được:
-
A.
\(\left( {x - 4} \right)\left( {x - 5} \right)\).
-
B.
\(\left( {x - 4} \right)\left( {x - 3} \right)\).
-
C.
\(\left( {x - 4} \right)\left( {x + 3} \right)\).
-
D.
\(\left( {x - 4} \right)\left( {x + 5} \right)\).
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
-
A.
\(7xy\left( {2x - 3y + 4xy} \right)\).
-
B.
\(xy\left( {14x - 21y + 28xy} \right)\).
-
C.
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
-
D.
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).