Tính thể tích khối rubik có dạng hình chóp tam giác đều (hình 4). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh \(6\)cm và chiều cao \(3\sqrt 3\)cm; chiều cao của khối rubik bằng \(2\sqrt 6\)cm.

Sử dụng công thức tính thể tích hình chóp tam giác đều
Diện tích đáy là: \(\frac{{(3\sqrt 3).6}}{2} = 9\sqrt 3\) (\(c{m^2}\))
Thể tích của khối rubik là: \(\frac{1}{3}.9\sqrt 3.2\sqrt 6 = 18\sqrt 2\) (\(c{m^3}\))

Các bài tập cùng chuyên đề
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{81\sqrt 3 }}{4}c{m^3}\).
-
B.
\(\frac{{27\sqrt 3 }}{8}c{m^3}\).
-
C.
\(\frac{{81\sqrt 3 }}{8}c{m^3}\).
-
D.
\(\frac{{27\sqrt 3 }}{4}c{m^3}\).
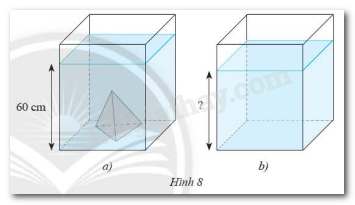
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60\)cm và \(30\)cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270c{m^2}\), chiều cao \(30\)cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mực nước là \(60\)cm. Khi lấy khối đá ra thì mực nước của bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể?
Cho một hình chóp tam giác đều có diện tích đáy bằng 15 cm2 và chiều cao 8 cm. Tính thể tích của hình chóp tam giác đều đó.
Dùng một “phễu đong” dạng hình chóp tam giác đều với cạnh đáy dài \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28a) đong các hạt đỗ đến ngang miệng rồi đổ vào một hộp có dạng hình lăng trụ đứng tam giác với đáy là tam giác đều cạnh \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28b). Cần đong bao nhiêu lần như vậy để đổ đầy hộp?

Tính diện tích đáy của một hình chóp tam giác đều có chiều cao bằng \(7,5cm\)và thể tích bằng \(62,5c{m^3}.\)
Thể tích của hình chóp tam giác đều sẽ thay đổi như thế nào nếu:
a) Độ dài cạnh đáy không đổi còn chiều cao tăng gấp ba lần?
b) Độ dài cạnh đáy tăng gấp hai lần còn chiều cao không đổi?
Tính thể tích của hình chóp tam giác đều có chiều cao 34cm và tam giác đáy có cạnh 16cm, chiều cao $8\sqrt{3}cm$. (Làm tròn kết quả đến hàng phần mười.)
Một chiếc gàu có dạng hình chóp tam giác đều và một chiếc bình có dạng hình lăng trụ đứng tam giác có cùng diện tích đáy. Người ta đổ 6 gàu nước vào bình và đo mực nước trong bình tăng thêm 1,2m. Tính chiều cao của chiếc gàu.
Cho hình chóp tam giác đều có diện tích đáy bằng \(36c{m^2}\) và chiều cao bằng 9cm. Thể tích của hình chóp này là
A. \(54c{m^3}\)
B. \(72c{m^3}\)
C. \(108c{m^3}\)
D. \(216c{m^3}\)
Cho hình chóp tam giác đều có thể tích bằng 30 cm3 và chiều cao bằng 12 cm. Tính diện tích đáy của hình chóp tam giác đều đó.
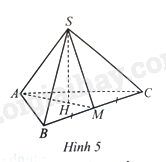
Cho hình chóp tam giác đều \(S.ABC\) có độ dài cạnh đáy bằng 9 cm, \(SH\) là chiều cao. Gọi \(M\) là trung điểm của \(BC\) (Hình 5). Tính thể tích của hình chóp \(S.ABC\), biết \(H\) là trọng tâm của tam giác \(ABC\), \(AH = \frac{{\sqrt 3 }}{3}AB\) và \(SH = 2AH\).
Cho hình chóp tam giác đều có thể tích bằng \(32\sqrt 3 c{m^3}\) và diện tích đáy bằng \(4\sqrt 3 c{m^2}\). Tính chiều cao của hình chóp tam giác đều đó.
-
A.
\(S = \frac{h}{V}\)
-
B.
\(S = \frac{V}{h}\)
-
C.
\(S = \frac{3V}{h}\)
-
D.
\(S = \frac{3h}{V}\)
Một khối Rubic có dạng hình chóp tam giác đều. Biết chiều cao khoảng \(5,88 cm\), thể tích của khối Rubic là \(44,002 cm^{3}\). Tính diện tích đáy của khối Rubic.
Một hình chóp tam giác đều có thể tích là \(12\sqrt 3 \,\,c{m^3}\), diện tích đáy là \(9\sqrt 3 \,\,c{m^2}\). Tính chiều cao của hình chóp tam giác đều đó.
Cho hình chóp tam giác đều S.MNP như H.10.15
a) Tính diện tích tam giác MNP
b) Tính thể tích hình chóp S.MNP, biết \(\sqrt {27} = 5,2\)

Tính thể tích của hình chóp tam giác đều S.ABC, biết diện tích đáy của nó bằng 15,6 cm2, chiều cao bằng 10 cm
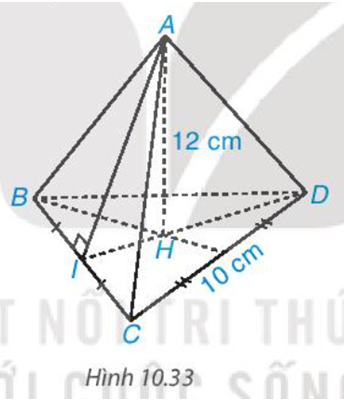
Tính thể tích hình chóp tam giác đều A.BCD, biết \(\sqrt {75} = 8,66\)
Một hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S là:
A. \(S = \frac{h}{V}\)
B. \(S = \frac{V}{h}\)
C. \(S = \frac{{3V}}{h}\)
D. \(S = \frac{{3h}}{V}\)
Hình chóp tam giác đều \(S.ABC\) có thể tích là \(225\,cm^{3}\). Tính chiều cao \(SO\) của hình chóp tam giác đều \(S.ABC\) biết diện tích tam giác \(ABC\) là \(135\,cm^{2}\).
-
A.
\(\frac{5}{3}\, cm\);
-
B.
\(3\, cm\);
-
C.
\(4\, cm\);
-
D.
\(5\, cm\).
Cho hình chóp tam giác đều có diện tích đáy là \(18c{m^2}\) và chiều cao là \(5cm\). Thể tích của hình chóp tam giác đều là:
-
A.
\(23c{m^3}\).
-
B.
\(45c{m^3}\).
-
C.
\(30c{m^3}\).
-
D.
\(90c{m^3}\).
Cho một hình chóp tam giác đều có diện tích đáy là \(15c{m^2}\) và chiều cao là 8cm. Khi đó thể tích của hình chóp tam giác đều đó là:
-
A.
\(48c{m^3}\).
-
B.
\(30c{m^3}\).
-
C.
\(60c{m^3}\).
-
D.
\(40c{m^3}\).
Một khối gỗ trang trí có dạng hình chóp tam giác đều. Diện tích đáy của khối gỗ bằng \(43c{m^2},\) chiều cao của khối gỗ bằng 8cm. Hỏi thể tích của khối gỗ bằng bao nhiêu?
Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8). Hãy tính thể tích của hình chóp S.MNP. Cho biết $\sqrt{48}\approx 6,9$

Hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S bằng:
A. \(S = \frac{h}{V}\)
B. \(S = \frac{V}{h}\)
C. \(S = \frac{{3V}}{h}\)
D. \(S = \frac{{3h}}{V}\)
Một hình chóp tam giác đều có diện tích đáy bằng \(4c{m^2}\), thể tích bằng \(8c{m^3}\). Chiều cao của khối chóp bằng:
A. 8cm
B. 9cm
C. 4cm
D. 6cm
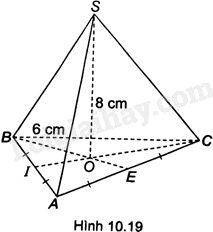
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6cm, chiều cao 8cm như Hình 10.19. Tính thể tích hình chóp, biết \(\sqrt {27} \approx 5,2\)
Thể tích của hình chóp tam giác đều bằng:
A. Tích của diện tích đáy với chiều cao của nó.
B. Nửa tích của diện tích đáy với chiều cao của nó.
C. \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
D. Tích của trung đoạn với chu vi đáy.
Một hình chóp tam giác đều có diện tích đáy bằng 30cm2, chiều cao bằng 6cm. Thể tích của hình chóp tam giác đều này bằng:
A. 180cm3.
B. 56cm3.
C. 36cm3.
D. 60cm3.
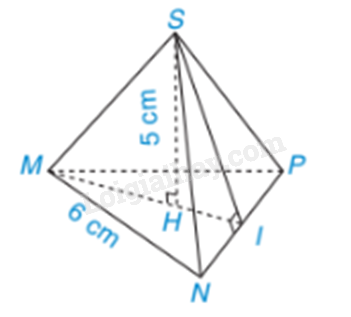
Cho hình chóp tam giác đều S.MNP có độ dài cạnh đáy băng 6cm, chiều cao bằng 5cm. (H.10.4)
a) Tính diện tích tam giác MNP.
b) Tính thể tích hình chóp S.MNP, biết \(\sqrt {27} \approx 5,2\)







Danh sách bình luận