Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N.
Chứng minh DM + BN = MN.
Chứng minh: MD = MP; ∆ADM = ∆APM (cạnh huyền – góc nhọn).
Suy ra MD = MP (hai cạnh tương ứng).
Ta có MP + PN = MN mà MD = MP
Do đó DM + BN = MN.
Vì ABCD là hình vuông nên \(\widehat D = {90^o}\)
Đường thẳng qua M vuông góc với AE cắt BC tại N nên \(\widehat {APM} = {90^o}\)
Do đó \(\widehat D = \widehat {APM} = {90^o}\)
Xét ∆ADM và ∆APM có:
\(\widehat D = \widehat {APM} = {90^o}\) (chứng minh trên)
Cạnh AM chung
\(\widehat {MA{\rm{D}}} = \widehat {MAP}\)(vì AM là tia phân giác của \(\widehat {DAP}\)).
Do đó ∆ADM = ∆APM (cạnh huyền – góc nhọn).
Suy ra MD = MP (hai cạnh tương ứng).
Chứng minh tương tự ta có BN = PN.
Ta có MP + PN = MN mà MD = MP; BN = PN (chứng minh trên)
Do đó DM + BN = MN.
Các bài tập cùng chuyên đề
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)
a) Mỗi hình vuông có là một hình chữ nhật hay không?
b) Mỗi hình vuông có là một hình thoi hay không?
Cho hình vuông ABCD. Tính số đo các góc CAB, DAC.
Từ tính chất của hình chữ nhật và hình thoi, em hãy nêu tính chất của đường chéo hình vuông.
Tính độ dài cạnh của hình vuông có đường chéo bằng \(5\,cm.\)
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN.
Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.
Cho hình vuông ABCD với tâm O và có cạnh bằng 2cm. Hai tia Ox, Oy tạo thành góc vuông. Tính diện tích của phần hình vuông nằm bên trong góc xOy.
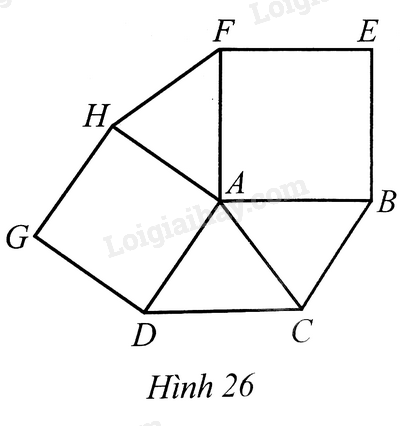
Cho hình bình hành \(ABCD\). Ở phía ngoài hình bình hành, vẽ các hình vuông \(ABEF\) và \(ADGH\) (Hình 26). Chứng minh:
a) \(\Delta AHF = \Delta ADC\)
b) \(AC \bot HF\).
