Giả sử chi phí vận chuyển x sản phẩm đến nơi tiêu thụ của một công ty được tính bởi công thức \(C = 2x_{}^2 - 40x + 480\) (nghìn đồng). Xác định số sản phẩm được vận chuyển đến nơi tiêu thụ khi chi phí vận chuyển là 480 000 đồng.

Giải các phương trình sau:

a) \(\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;\)

b) \({x^2} - 3x = 2x - 6.\)

Giải bài toán ở tình huống mở đầu.

Tình huống mở đầu: Trong một khu vườn hình vuông có cạnh bằng 15m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là \(169{m^2}\) thì bề rộng x của lối đi là bao nhiêu?

Giải các phương trình sau:

a) \(\left( {{x^2} - 4} \right) + x\left( {x - 2} \right) = 0;\)

b) \({\left( {2x + 1} \right)^2} - 9{x^2} = 0.\)

Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là \(100{m^2}.\) Hỏi x bằng bao nhiêu mét?

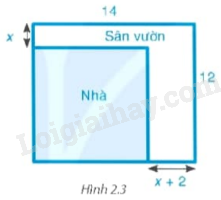
Giải các phương trình sau:

a) \(2\left( {x + 1} \right) = \left( {5x - 1} \right)\left( {x + 1} \right);\)

b) \(\left( { - 4x + 3} \right)x = \left( {2x + 5} \right)x.\)

Giải các phương trình sau:

a) \({\left( {3x - 1} \right)^2} - {\left( {x + 2} \right)^2} = 0;\)

b) \(x\left( {x + 1} \right) = 2\left( {{x^2} - 1} \right).\)

Giải các phương trình:

a) \(2x\left( {x + 6} \right) + 5\left( {x + 6} \right) = 0\);

b) \(x\left( {3x + 5} \right) - 6x - 10 = 0\).

Giải các phương trình:

a) \(3x(x - 4) + 7(x - 4) = 0\);

b) \(5x(x + 6) - 2x - 12 = 0\);

c) \({x^2} - x - (5x - 5) = 0\);

d) \({(3x - 2)^2} - {(x + 6)^2} = 0\).

Giải các phương trình:

a) (5x + 2)(2x – 7) = 0

b) \(\left( {\frac{1}{2}x + 5} \right)\left( { - \frac{2}{3}x - \frac{4}{3}} \right) = 0\)

c) \({y^2} - 5y + 2(y - 5) = 0\)

d) \(9{x^2} - 1 = (3x - 1)(2x + 7)\)

Trong một khu đất có dạng hình vuông, người ta dành một mảnh đất có dạng hình chữ nhật ở góc khu đất làm bể bơi. Biết diện tích của bể bơi bằng \(1250{m^2}\). Độ dài cạnh của khu đất bằng bao nhiêu mét?

Giải các phương trình:

a. \({x^2} - 10x + 25 = 5\left( {x - 5} \right)\);

b. \(4{x^2} - 16 = 5\left( {x + 2} \right)\).

Giải các phương trình:

a. \(\left( {9x - 4} \right)\left( {2x + 5} \right) = 0\);

b. \(\left( {1,3x + 0,26} \right)\left( {0,2x - 4} \right) = 0\);

c. \(2x\left( {x + 3} \right) - 5\left( {x + 3} \right) = 0\);

d. \({x^2} - 4 + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\).

Trên một mảnh đất có dạng hình chữ nhật với chu vi bằng 52m. Trên mảnh đất đó, người ta làm một vườn có dạng hình chữ nhật có diện tích là \(112{m^2}\) và một lối đi xung quanh vườn rộng 1m (Hình 2). Tính các kích thước của mảnh đất đó.

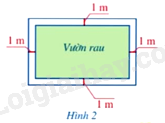
Giải các phương trình:

a. \(\left( {3x + 7} \right)\left( {4x - 9} \right) = 0\);

b. \(\left( {5x - 0,2} \right)\left( {0,3x + 6} \right) = 0\);

c. \(x\left( {2x - 1} \right) + 5\left( {2x - 1} \right) = 0\);

d. \({x^2} - 9 - \left( {x + 3} \right)\left( {3x + 1} \right) = 0\);

e. \({x^2} - 10x + 25 = 3\left( {5 - x} \right)\);

g. \(4{x^2} = {\left( {x - 12} \right)^2}\)

Hình bên mô tả một pháo sáng được phóng từ một bè cứu sinh trên biển. Độ cao \(h\left( m \right)\) của pháo sáng so với mặt nước biển được tính bởi công thức \(h = 30,48t - 4,8768{t^2}\), trong đó \(t\left( s \right)\) là thời gian sau khi pháo sáng được bắn. Sau bao lâu pháo sáng rơi xuống biển?

Giải các phương trình sau:

a. \(\left( {12 - 4x} \right)\left( {5x + 6} \right) = 0\);

b. \(\left( {4x + 1} \right)_{}^2 - \left( {2x - 3} \right)_{}^2 = 0\).

Giải phương trình \(\left( {5x + 8} \right)\left( {6x - 1} \right) = \left( {3x - 4} \right)\left( {6x - 1} \right)\).

Trả lời câu hỏi nêu trong phần Khởi động.

Câu hỏi khởi động: Hình bên mô tả một pháo sáng được phóng từ một bè cứu sinh trên biển. Độ cao \(h\left( m \right)\) của pháo sáng so với mặt nước biển được tính bởi công thức \(h = 30,48t - 4,8768{t^2}\), trong đó \(t\left( s \right)\) là thời gian sau khi pháo sáng được bắn. Sau bao lâu pháo sáng rơi xuống biển?

Phân tích vế trái thành nhân tử rồi giải phương trình:

a. \(3x\left( {x - 6} \right) + 8\left( {x - 6} \right) = 0\);

b. \(\left( {4x_{}^2 - 9} \right) - \left( {x + 2} \right)\left( {3 - 2x} \right) = 0\).

Giải các phương trình sau bằng cách đưa về dạng tích:

a) \(x\left( {2x - 10} \right) = 4x\left( {x - 6} \right)\).

b) \(4x + 12 = \left( {x + 3} \right)\left( {7 - 5x} \right)\).

c) \(\left( {{x^2} + 4x + 4} \right) - 25 = 0\).

d) \(9{x^2} - 6x + 1 = {x^2}\).

Độ cao \(h\) (m) của một viên đá so với mực nước biển khi được ném từ đỉnh của một vách đá được tính bởi công thức \(h =  - 5{t^2} + 15t + 20\), trong đó \(t\left( s \right)\) là thời gian kể từ lúc viên đá bắt đầu được ném. Khi nào viên đá đạt độ cao 20m so với mực nước biển?

Một công ty thiết kế nội thất sản xuất ra hai loại ghế là ghế bành và ghế dài từ hai loại nguyên liệu là gỗ và vải. Số đơn vị nguyên liệu cần dùng để tạo ra một chiếc ghế mỗi loại được cho trong bảng sau:

Hỏi có bao nhiêu chiếc ghế mỗi loại được sản xuất nếu sử dụng hết 1 600 đơn vị gỗ và 1 400 đơn vị vải?

Tổng các nghiệm của phương trình \(\left( {x - 1} \right)\left( {2x - 1} \right) = \left( {x - 1} \right)\left( {x + 2} \right)\) là:

A. 1

B. 2

C. 3

D. 4

Cho phương trình \(4{x^2} - 4x + 1 = {x^2}\). Khẳng định nào sau đây là đúng?

A. Phương trình đã cho có đúng hai nghiệm.

B. Phương trình đã cho có đúng một nghiệm.

C. Phương trình đã cho có vô số nghiệm.

D. Phương trình đã cho vô nghiệm.

Cho phương trình \(5 - 6\left( {2x - 3} \right) = x\left( {3 - 2x} \right) + 5\). Chọn khẳng định đúng.

Tích các nghiệm của phương trình \({x^3} - 3{x^2} - x + 3 = 0\) là

Số nghiệm của phương trình \(\left( {{x^2} + 9} \right)\left( {x - 1} \right) = \left( {{x^2} + 9} \right)\left( {x + 3} \right)\) là

Nghiệm nhỏ nhất của phương trình \({\left( { - \dfrac{1}{2}x + 1} \right)^2} = {\left( {\dfrac{3}{2}x - 1} \right)^2}\) là

Tập nghiệm của phương trình \(\left( {{x^2} - x - 1} \right)\left( {{x^2} - x + 1} \right) = 3\) là

Tìm \(m\) để phương trình \(\left( {2m - 5} \right)x - 2{m^2} - 7 = 0\) nhận \(x = - 3\) làm nghiệm.