Chú hề trên sân khấu thường có trang phục như Hình 27a. Mũ của chủ hề có dạng hình nón. Có thể mô phỏng cấu tạo, kích thước chiếc mũ của chú hề như Hình 27b.
a) Để phủ kín mặt ngoài chiếc mũ của chú hề như Hình 27b cần bao nhiều centimét
vuông giấy màu (không tính phần mép dán và làm tròn kết quả đến hàng đơn vị)?
b) Hỏi thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình 27b bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm)?

a) Mặt ngoài là diện tích xung quanh + diện tích phần vành chiếc mũ.
- Sử dụng công thức tính diện tích xung quanh hình nón: \(S_{xq} = \pi rl\)
- Sử dụng công thức tính diện tích hình vành khuyên: \(S = \pi (R^2 - r^2)\)
b) Sử dụng định lí Pythagore để tính chiều cao.
Áp dụng công thức tính thể tích hình nón \(V = \frac{1}{3}\pi {r^2}h.\)

a) Gọi h là chiều cao, r là bán kính đáy, l là đường sinh chiếc mũ.
Bán kính đáy chiếc mũ là:
\(r = \left( {26 - 3.2} \right):2 = 10\left( {cm} \right).\)
Mặt ngoài là diện tích xung quanh chiếc mũ, ta có:
\({S_{xq}} = \pi rl = \pi .10.30 \approx 942\left( {c{m^2}} \right).\)
Bán kính của đường viền lớn bên ngoài vành mũ là:
\(26:2 = 13 (cm)\)
Diện tích phần vành mũ là:
\(\pi(13^2 - 10^2) \approx 216,66 (cm)\)
Vậy để phủ kín mặt ngoài chiếc mũ của chú hề như Hình 27b cần khoảng:
\(942 + 216,66 = 1158,66 \approx 1159\) \(c{m^2}\) giấy màu.
b) Chiều cao của chiếc mũ hình nón là:
\(\sqrt {30^2 - 10^2} = 20 \sqrt 2 (cm)\)
Thể tích phần có dạng hình nón của chiếc mũ chú hề là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.10^2}.20 \sqrt 2 \approx 2960,42 (c{m^3}).\)
Vậy thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình 27b khoảng \(2960,42 (c{m^3}).\)

Các bài tập cùng chuyên đề
Tính diện tích xung quanh và thể tích của một hình nón có độ dài đường sinh bằng 13cm và chiều cao bằng 12cm.
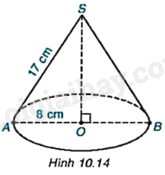
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết \(OA = 8cm\), \(SA = 17cm\) (H.10.14).
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
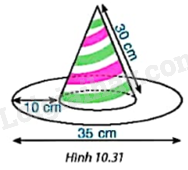
Chiếc mũ của chú hề với các kích thước như Hình 10.31. Hãy tính tổng diện tích vải cần để làm chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần chục của \(c{m^2}\)).
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm (H.10.34).
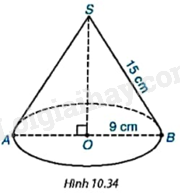
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
Mái nhà hát Cao Văn Lầu và Trung tâm triển lãm Văn hóa Nghệ thuật tỉnh Bạc Liêu có hình dáng ba chiếc nón lá lớn nhất Việt Nam (H.10.40). Tính diện tích một mái nhà hình nón có đường kính bằng 45m và chiều cao bằng 24m (làm tròn kết quả đến hàng đơn vị của \({m^2}\)).

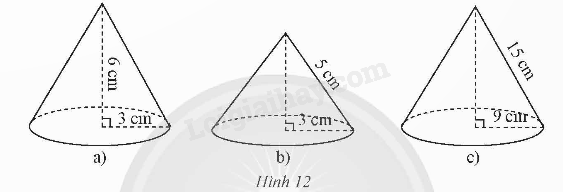
Hãy cho biết chiều cao, bán kính đáy, độ dài đường sinh và diện tích xung quanh của mỗi hình nón sau:
Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
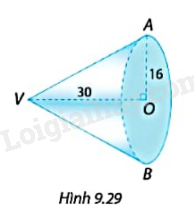
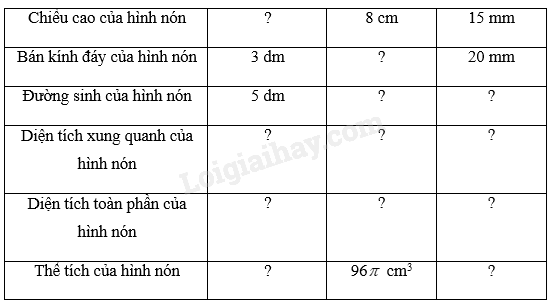
Tìm các số và đơn vị thích hợp để hoàn thành Bảng 9.2.
Tính diện tích bìa cần dùng (theo centimet vuông) để làm một chiếc mũ sinh nhật có dạng hình nón như Hình 9.30 với đường kính đáy 22 cm và chiều cao 18 cm (bỏ qua các mép nối và phần thừa, làm tròn kết quả đến centimet vuông).

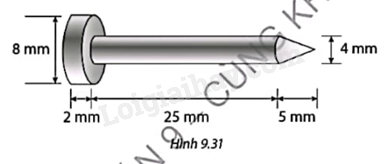
Thả 10 chiếc đinh có kích thước như Hình 9.31 vào một cốc nước thuỷ tinh. Đinh chìm hẳn xuống và nước trong cốc không bị trần ra ngoài. Hỏi thể tích nước trong cốc tăng thêm bao nhiêu mililit (làm tròn kết quả đến hàng phần mười)?
Tính bán kính đáy của hình nón có chiều cao 12 cm, đường sinh dài 13 cm.
A. 5 cm
B. 6 cm
C. 10 cm
D. 6,5 cm
Một chi tiết máy có hình như phía dưới. Độ dài các cạnh \(SO = 4{\rm{cm}};\) \(SS' = 6{\rm{cm}}\) và \(OA = 2{\rm{cm}}\).
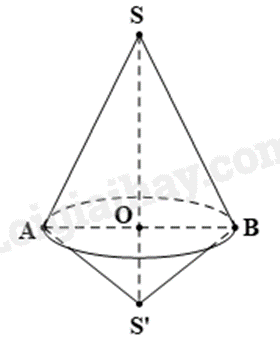
a) Độ dài đoạn thẳng \(S{\rm{'}}O\) là \(2{\rm{cm}}\).
b) Thể tích của hình nón có đường cao \(SO\) là \({V_1} = 16\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
c) Thể tích của hình nón có đường cao \(S{\rm{'}}O\) là \({V_2} = \frac{8}{3}\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
d) Nếu một ống hình trụ có đường cao bằng \({\rm{2cm}}\) và thể tích bằng thể tích của chi tiết máy thì diện tích xung quanh của hình trụ là \({S_{xq}} = 4\sqrt 2 \pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Một chi tiết máy bằng đồng được tạo bởi hình chóp có đường cao \(SO\) bỏ phần hình chóp có đường cao \(AO\) như hình phía dưới. Độ dài các cạnh \(SO = 6{\rm{cm}};\) \(SA = 3{\rm{cm}}\) và \(OB = 3{\rm{cm}}\).
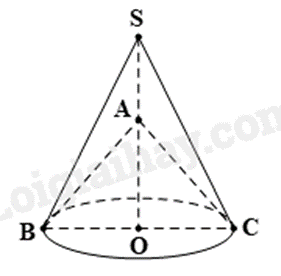
a) Độ dài đoạn thẳng \(AO\) là \({\rm{3cm}}\).
b) Thể tích của hình nón có đường cao \(AO\) là \({V_1} = 18\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
c) Biết khối lượng riêng của đồng là \(D = 8,96{\rm{g/c}}{{\rm{m}}^3}\). Khối lượng đồng cần làm chi tiết máy làm tròn đến số thập phân thứ hai là \(253,21{\rm{g}}\). (lấy \(\pi = 3,14\))
d) Một hình trụ có thể tích gấp 8 lần thể tích chi tiết máy. Diện tích xung quanh bé nhất của hình trụ có thể đựng được chi tiết máy là \(\pi \sqrt[3]{{18}}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Một hình nón có bán kính đáy bằng \(2\,cm\), chiều cao hình nón là \(h\,\,\left( {cm} \right)\).
a) Độ dài đường sinh của hình nón là \(\sqrt {{h^2} + 4} \,\,\,\left( {cm} \right)\).
b) Thể tích của hình nón là \(4\pi h\,\,\,\left( {c{m^3}} \right)\).
c) Diện tích toàn phần của hình nón là \({S_{tp}} = \pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\,\,\left( {c{m^2}} \right)\).
d) Chiều cao của hình nón trên bằng đường kính một hình cầu, diện tích toàn phần hình nón bằng diện tích mặt cầu. Chiều cao của hình nón là \(2\,\sqrt 3 \,cm\).
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:

Cho tam giác OAB vuông tại O có AB = 37 cm, OA = 12 cm. Tính diện tích xung quanh và thể tích của hình tạo thành khi quay tam giác OAB một vòng quanh cạnh OB.
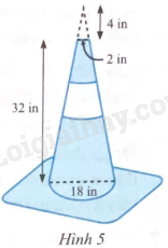
Một cọc tiêu có dạng hình nón bị cắt đi phần ở trên cũng có dạng hình nón như Hình 5.
a) Tính diện tích xung quanh của cọc tiêu theo đơn vị in2 (không tính phần đế).
b) Tính thể tích của cọc tiêu theo đơn vị in3 (không tính phần đế).
(Làm tròn kết quả đến hàng đơn vị của in2, in3).
Một hình nón có diện tích xung quanh và diện tích toàn phần lần lượt bằng 65π cm2, 115π cm2. Hỏi chiều cao của hình nón đó bằng bao nhiêu centimét (làm tròn kết quả đến hàng đơn vị).
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết \(OA = 8cm\), \(SA = 17cm\).
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
Tam giác ABC cân tại A, đường cao AH, có \(AB = 5cm,BC = 8cm\). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón.
a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^3}\)).
b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^2}\)).
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm.
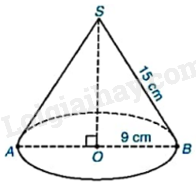
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
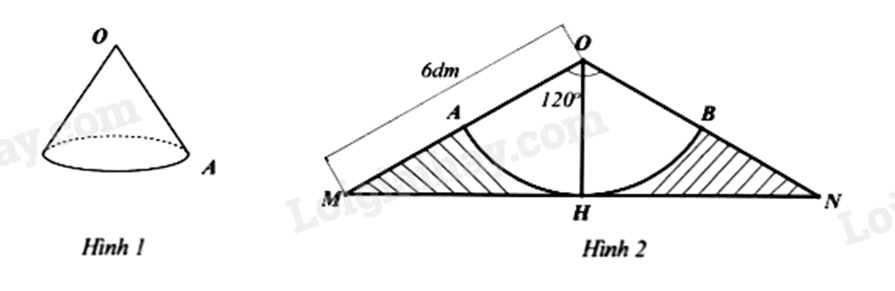
a) Tính diện tích tôn cần dùng để làm chiếc gàu? (kết quả làm tròn 1 chữ số thập phân)
b) Hỏi khi múc đầy thì chiếc gàu chứa được bao nhiêu lít nước? (kết quả làm tròn đến hàng đơn vị). Biết \(V = \frac{1}{3}\pi {r^2}h\), trong đó h là chiều cao hình nón, r là bán kính mặt đáy hình nón.







Danh sách bình luận