Giá trị nhỏ nhất của hàm số $y = 2x + \cos x$ trên đoạn $\left[ {0;1} \right]$ là :

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là

Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M =  - 2$. Chọn khẳng định đúng:

Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:

Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to  + \infty } f(x) =  + \infty ;\mathop {\lim }\limits_{x \to  - \infty } f(x) =  - \infty$ , khi đó:

Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$

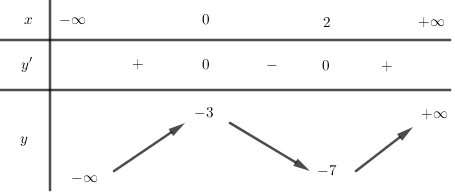
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:

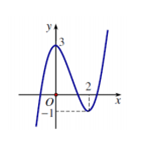
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?

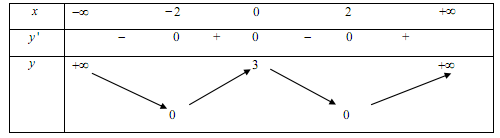
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

Khẳng định nào sau đây là khẳng định đúng?

Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$

Tìm GTLN và GTNN của hàm số $y = {x^5} - 5{x^4} + 5{x^3} + 1$ trên đoạn $\left[ { - 1;2} \right]$

Giá trị lớn nhất của hàm số $f\left( {\text{x}} \right) = \dfrac{{6 - 8{\text{x}}}}{{{x^2} + 1}}$ trên tập xác định của nó là:

Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:

Cho hàm số $y = x + \dfrac{1}{x}.$ Giá trị nhỏ nhất của hàm số trên khoảng $\left( {0;\, + \infty } \right)$ là:

Cho hàm số $y = \dfrac{{2mx + 1}}{{m - x}}.$ Giá trị lớn nhất của hàm số trên $\left[ {2;3} \right]$ bằng $\dfrac{{ - 1}}{3}$ khi m bằng:

Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:

Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:

Có bao nhiêu số nguyên $m \in \left[ { - 5;5} \right]$ để $\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2$.

Cho hai số thực $x,\,y$ thỏa mãn ${x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10}  = \sqrt {6 + 4x - {x^2}}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức $T = \left| {\sqrt {{x^2} + {y^2}}  - a} \right|$. Có bao nhiêu giá trị nguyên thuộc đoạn $\left[ { - 10;\,10} \right]$ của tham số $a$ để $M \ge 2m$?

Cho $f\left( x \right)$ mà đồ thị hàm số $y = f'\left( x \right)$ như hình vẽ bên

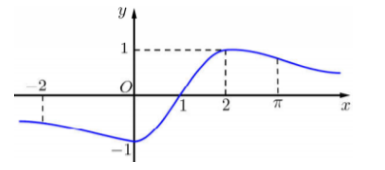
Bất phương trình $f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m$ nghiệm đúng với mọi $x \in \left[ { - 1;3} \right]$ khi và chỉ khi:

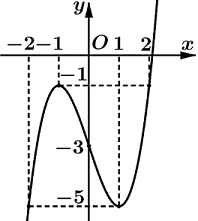
Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất $m$ và giá trị lớn nhất $M$ của hàm số $y = f\left( x \right)$ trên đoạn $\left[ { - 2;2} \right]$.