Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
-
A.
$m = 2$
-
B.
$m = 5$
-
C.
$m = 3$
-
D.
$m = 4$
Sử dung BĐT Cauchy cho hai số không âm \(a + b \ge 2\sqrt {ab} \)
Cách 1:
Xét \(y' = 1 - \frac{4}{{{{(x - 1)}^2}}} = 0 \Leftrightarrow {x^2} - 2x + - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = - 1}\end{array}} \right.\)
Bảng biến thiên trên \((1; + \infty )\):
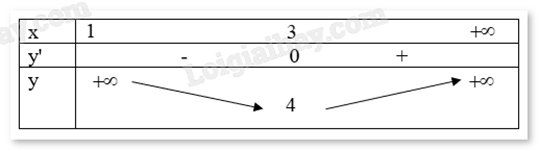
Vậy m = 4 khi x = 3.
Cách 2:
${\rm{\;}}x > 1 \Leftrightarrow x - 1 > 0$
$ \Rightarrow y = x - 1 + \dfrac{4}{{x - 1}} \ge 2\sqrt {\left( {x - 1} \right).\dfrac{4}{{x - 1}}} = 2.2 = 4$
Dấu bằng xảy ra $ \Leftrightarrow x - 1 = \dfrac{4}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow x = 3$.
Vậy GTNN của hàm số là $m=4$ khi $x=3$.
Đáp án : D
Các em cũng có thể đạo hàm và tìm GTNN như sau:
\(\begin{array}{l}y' = 1 - \frac{4}{{{{\left( {x - 1} \right)}^2}}}\\y' = 0 \Leftrightarrow 1 - \frac{4}{{{{\left( {x - 1} \right)}^2}}} = 0\\ \Leftrightarrow 1 = \frac{4}{{{{\left( {x - 1} \right)}^2}}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 2\\x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left( {1; + \infty } \right)\\x = - 1 \notin \left( {1; + \infty } \right)\end{array} \right.\end{array}\)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\) ta thấy \({y_{\min }} = y\left( 3 \right) = 4\).








Danh sách bình luận