a) Thực hiện các phép tính cho trên bảng trong Hình 1.
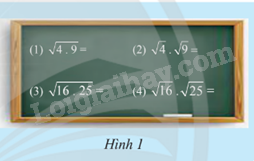
b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm?
Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}} = a\). ( a > 0)
a)
(1) \(\sqrt {4.9} = \sqrt {36} = \sqrt {{{\left( 6 \right)}^2}} = 6\)
(2) \(\sqrt 4 .\sqrt 9 = \sqrt {{2^2}} .\sqrt {{3^2}} = 2.3 = 6\)
(3) \(\sqrt {16.25} = \sqrt {400} = \sqrt {{{\left( {20} \right)}^2}} = 20\)
(4) \(\sqrt {16} .\sqrt {25} = \sqrt {{4^2}} .\sqrt {{5^2}} = 4.5 = 20\)
b) Căn bậc hai của tích hai số không âm bằng tích các căn bậc hai của hai số không âm.
Các bài tập cùng chuyên đề
Kết quả của phép tính $\sqrt {2,5} .\sqrt {14,4} $ là?
Tính và so sánh: \(\sqrt {100} .\sqrt 4 \) và \(\sqrt {100.4} .\)
Tính:
a) \(\sqrt {12} .\left( {\sqrt {12} + \sqrt 3 } \right);\)
b) \(\sqrt 8 .\left( {\sqrt {50} - \sqrt 2 } \right);\)
c) \({\left( {\sqrt 3 + \sqrt 2 } \right)^2} - 2\sqrt 6 .\)
Thực hiện phép tính:
a) \(\sqrt 3 .\left( {\sqrt {192} - \sqrt {75} } \right);\)
b) \(\frac{{ - 3\sqrt {18} + 5\sqrt {50} - \sqrt {128} }}{{7\sqrt 2 }}.\)
Thay mỗi ? bằng các số thích hợp:
a) \(\sqrt {50} = \sqrt ? .\sqrt 2 = ?.\sqrt 2 \)
b) \(\sqrt {3.{{( - 4)}^2}} = \sqrt ? .\sqrt 3 = ?.\sqrt 3 \)
c) \(3\sqrt 2 = \sqrt ? .\sqrt 2 = \sqrt ? \)
d) \( - 2\sqrt 5 = - \sqrt ? .\sqrt 5 = - \sqrt ? \)
Tính
a) \(\sqrt {0,16.64} \)
b) \(\sqrt {8,{{1.10}^3}} \)
c) \(\sqrt {12.250.1,2} \)
d) \(\sqrt {28} .\sqrt 7 \)
e) \(\sqrt {4,9} .\sqrt {30} .\sqrt {12} \)
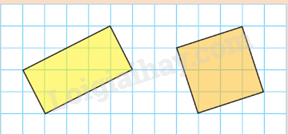
Tính diện tích của hình chữ nhật và hình vuông trong hoạt động khởi động. Biết mỗi ô vuông nhỏ có độ dài cạnh là 1. Diện tích của hai hình đó bằng nhau không?
Tính
a) \(\sqrt {16.0,25} \)
b) \(\sqrt {{2^4}.{{( - 7)}^2}} \)
c) \(\sqrt {0,9} .\sqrt {1000} \)
d) \(\sqrt 2 .\sqrt 5 .\sqrt {40} \)
So sánh: \(\sqrt {4.25} \) và \(\sqrt 4 .\sqrt {25} \).
Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:
a. \(\sqrt {25.121} \);
b. \(\sqrt 2 .\sqrt {\frac{9}{8}} \);
c. \(\sqrt {10} .\sqrt {5,2} .\sqrt {52} \).
Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:
a. \(\sqrt {36.81} \)
b. \(\sqrt {49.121.169} \)
c. \(\sqrt {{{50}^2} - {{14}^2}} \)
d. \(\sqrt {3 + \sqrt 5 } .\sqrt {3 - \sqrt 5 } \)
Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức \(v = \sqrt {2\lambda gd} \), trong đó \(v\left( {m/s} \right)\) là tốc độ của ô tô, \(d\left( m \right)\) là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, \(\lambda \) là hệ số cản lăn của mặt đường, \(g = 9,8m/{s^2}\). Nếu một ô tô để lại vết trượt dài khoảng 20m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu mét trên giây (làm tròn đến kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn của đường nhựa là \(\lambda = 0,7\).
Tính và so sánh
a) \(\sqrt {9.16} \) và \(\sqrt 9 .\sqrt {16} \)
b)\(\sqrt {4.25} \) và \(\sqrt 4 .\sqrt {25} \)
Rút gọn
a) \(\sqrt {\frac{7}{6}} .\sqrt {42} \);
b)\(\sqrt {0,16.36.225} \);
c) \(\sqrt {0,3} .\sqrt {51} .\sqrt {10} .\sqrt {17} \)
Tốc độ của xe ô tô và vết trượt của bánh xe trên mặt đường khi phanh gấp liên hệ với nhanh bởi công thức\(v = \sqrt {20kl} \), trong đó v (m/s) là tốc độ của xe ô tô khi phanh gấp, k là hệ số ma sát giữa bánh xe và mặt đường khi xe ô tô phanh và \(l\) (m) là độ dài vết trượt của bánh xe trên mặt đường.
a) Một ô tô đang chạy trên đường thì phanh gấp và tạo ra một vết trượt của bánh xe dài 25 m. Hỏi tốc độ của ô tô khi phanh gấp là bao nhiêu, biết hệ số ma sát giữa bánh xe và mặt đường ở thời điểm đó là 0,8?
b) Nếu tốc độ của một ô tô khi phanh gấp là 15 m/s và hệ số ma sát giữa bánh xe và mặt đường ở thời điểm đó là 0,6 thì vết trượt của bánh xe dài bao nhiêu?
Một hình chữ nhật có chiều dài và chiều rộng lần lượt là \(\sqrt {56} cm\) và \(\sqrt {14} cm\). Tính diện tích của hình chữ nhật.
Kết quả của phép tính: \(\sqrt {1,25} .\sqrt {51,2} \) là?
Phép tính $\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} $ có kết quả là?
Phép tính \(\sqrt {{{12}^2}.{{\left( { - 11} \right)}^2}} \) có kết quả là?
Tính : \(P = 2\sqrt 2 \left( {\sqrt 3 - 2} \right) + {\left( {1 + 2\sqrt 2 } \right)^2} - 2\sqrt 6 - \sqrt {9 - \sqrt {17} } .\sqrt {9 + \sqrt {17} } \)
Tính \(M = \left( {4 + \sqrt {15} } \right)\left( {\sqrt {10} - \sqrt 6 } \right)\sqrt {4 - \sqrt {15} } \)\(+ \sqrt {3 - \sqrt 5 } \left( {\sqrt {10} - \sqrt 2 } \right)\left( {3 + \sqrt 5 } \right)\)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
Giá trị của biểu thức \(2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} \) là:
Giá trị của biểu thức \(\sqrt {125} - 4\sqrt {45} + 3\sqrt {20} - \sqrt {80} \) là:
Không dùng MTCT, tính giá trị của biểu thức sau: \(P = \sqrt {2 + \sqrt {2 + \sqrt 2 } } .\sqrt {2 - \sqrt {2 + \sqrt 2 } } .\sqrt {4 + \sqrt 8 } \).
Rút gọn biểu thức \(P = \frac{{3\sqrt {10} + \sqrt {20} - 3\sqrt 6 - \sqrt {12} }}{{\sqrt 5 - \sqrt 3 }}\).
So sánh \(\sqrt {\sqrt {6 + \sqrt {20} } } \) và \(\sqrt {\sqrt 6 + 1} \).
Viết các biểu thức sau dưới dạng \(\sqrt a \) (a là một số).
a) \(\sqrt 5 .\sqrt {11} \)
b) \(\sqrt {\frac{{10}}{3}} .\sqrt {\frac{3}{5}} \)
c) \(\sqrt 3 .\sqrt 5 .\sqrt 6 \)
d) \(\sqrt {\frac{6}{7}} .\sqrt {2,8} \)
a) \(\sqrt {{{74}^2} - {{70}^2}} \)
b) \(\sqrt {{{\left( {62,5{)^2} - (58,5} \right)}^2}} + \left( {\sqrt {11} - 2\sqrt 5 } \right)\left( {\sqrt {11} + 2\sqrt 5 } \right)\)
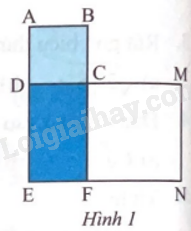
Cho Hình 1. Biết ABCD là hình vuông có diện tích bằng 6, CMNF là hình vuông có diện tích bằng 18. Tính diện tích hình chữ nhật CDEF.
