Giải các bất phương trình:
a) 3 – 0,2x < 13
b) \(\frac{1}{2} + \frac{x}{3} \ge \frac{1}{4}\)
c) 3 < \(\frac{{2x - 2}}{8}\)
d) \(\frac{{2x - 3}}{3} \le \frac{{3x - 2}}{4}\)
Dựa vào cách giải bất phương trình bậc nhất một ẩn:
Xét bất phương trình ax + b > 0 (a \( \ne \) 0)
- Cộng hai vế của bất phương trình với – b, ta được bất phương trình:
ax > - b
- Nhân hai vế của bất phương trình nhận được với \(\frac{1}{a}\):
+ Nếu a > 0 thì nhận được nghiệm của bất phương trình đã cho là \(x > - \frac{b}{a}\)
+ Nếu a < 0 thì nhận được nghiệm của bất phương trình đã cho là \(x < - \frac{b}{a}\)
a) 3 – 0,2x < 13
0,2x > - 10
x > - 50
Vậy nghiệm của bất phương trình là: x > - 50
b) \(\frac{1}{2} + \frac{x}{3} \ge \frac{1}{4}\)
\(\begin{array}{l}6 + 4x \ge 3\\4x \ge - 3\\x \ge \frac{{ - 3}}{4}\end{array}\)
Vậy nghiệm của bất phương trình là: \(x \ge \frac{{ - 3}}{4}\)
c) 3 < \(\frac{{2x - 2}}{8}\)
24 < 2x – 2
2x > 26
x > 13
Vậy nghiệm của bất phương trình là: x > 13
d) \(\frac{{2x - 3}}{3} \le \frac{{3x - 2}}{4}\)
4(2x – 3) \( \le \) 3(3x – 2)
8x – 12 \( \le \) 9x – 6
x \( \ge \) - 6
Vậy nghiệm của bất phương trình là: x \( \ge \) - 6

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(2{x^2} + 6x = 0\);
b) \(5{x^2} + 11x = 0\).
Độ cao h (mét) so với mặt đất của một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu \({v_o} = 19,6m/s\) cho bởi công thức \(h = 19,6t - 4,9{t^2}\), ở đó t là thời gian kể từ khi phóng (giây) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Hỏi sau bao lâu kể từ khi phóng, vật sẽ rơi trở lại mặt đất?
Bất phương trình 2x – 1 \( \le \) x + 4 có nghiệm là
A. x \( \le \) 5
B. x \( \ge \) 5
C. x \( \le \) -5
D. x < 5
Cho a > b, chứng minh:
a) a – 2 > b – 2
b) -5a < - 5b
c) 2a + 3 > 2b + 3
d) 10 – 4a < 10 – 4b
Tìm x sao cho:
a) Giá trị của biểu thức 2x + 1 không nhỏ hơn giá trị của biểu thức 3x – 5
b) Giá trị của biểu thức 2x + 1 không lớn hơn giá trị của biểu thức 3x – 5
Trong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời 12 câu hỏi của ban tổ chức. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng. Với mỗi câu hỏi, nếu trả lời đúng được cộng 5 điểm, trả lời sai bị trừ 2 điểm. Khi bắt đầu cuộc thi, mỗi thí sinh có sẵn 20 điểm. Thí sinh nào đạt từ 50 điểm trở lên sẽ được vào vòng thi tiếp theo. Hỏi thí sinh phải trả lời đúng ít nhất bao nhiêu câu thì được vào vòng tiếp theo?
Tìm lỗi sai trong các lời giải sau:
a) Giải bất phương trình – 3x > 9.
Ta có : - 3x > 9
x > 9 + 3
x > 12
Vậy nghiệm của bất phương trình là x > 12.
b) Giải bất phương trình \( - \frac{2}{3}\)x \( \le \) 5.
Ta có \( - \frac{2}{3}\)x \( \le \) 5
\(\left( { - \frac{2}{3}} \right)x.\left( { - \frac{3}{2}} \right) \le \left( { - \frac{3}{2}} \right)\)
\(x \le \frac{{ - 15}}{2}\).
Vậy nghiệm của bất phương trình là \(x \le \frac{{ - 15}}{2}\)
Một con cá heo nhảy lên khỏi mặt nước. Sau t(s) kể từ khi nhảy lên, cá heo ở độ cao h = 6t – 5t2 (m) so với mặt nước. Sau bao lâu con cá heo ấy lại quay trở về mặt nước?
Không dùng công thức nghiệm, tính tích các nghiệm của phương trình \(3{x^2} - 10x + 3 = 0\).
-
A.
\(3\)
-
B.
\(\dfrac{{10}}{3}\)
-
C.
\(1\)
-
D.
\( - 1\)
Cho phương trình: \(2{x^2} - 5x = 0\). Khẳng định nào sau đây là đúng?
A. Phương trình có nghiệm duy nhất \(x = 0\).
B. Phương trình có nghiệm duy nhất \(x = \frac{5}{2}\).
C. Phương trình có hai nghiệm là \(x = 0\) và \(x = \frac{5}{2}\).
D. Phương trình có hai nghiệm là \(x = 0\) và \(x = \frac{2}{5}\).
Độ cao h (mét) so với mặt đất của một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu \({v_o} = 19,6\left( {m/s} \right)\) cho bởi công thức \(h = 19,6t - 4,9{t^2}\), ở đó t (giây) là thời gian kể từ khi phóng (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Hỏi sau bao lâu kể từ khi phóng, vật sẽ rơi trở lại mặt đất?
Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình $6{x^2} - 7x = 0$.
-
A.
$ - \dfrac{7}{6}$
-
B.
$\dfrac{7}{6}$
-
C.
$\dfrac{6}{7}$
-
D.
$ - \dfrac{6}{7}$
Không dùng công thức nghiệm, giải phương trình \({x^2} + 5x + 4 = 0\), ta được tập nghiệm là:
-
A.
\(S = \left\{ {1; - 4} \right\}\)
-
B.
\(S = \left\{ { - 1;4} \right\}\)
-
C.
\(S = \left\{ { - 1; - 4} \right\}\)
-
D.
\(S = \left\{ {1;4} \right\}\)
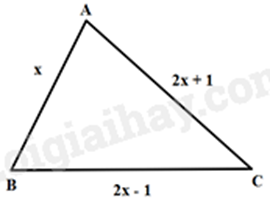
a) Viết biểu thức biểu diễn chu vi C của tam giác theo \(x\).
b) Tìm \(x\) để tam giác ABC vuông tại B?







Danh sách bình luận