Quả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính 24cm (H.10.35). Hãy tính:

a) Diện tích bề mặt quả bóng.
b) Thể tích của quả bóng.
+ Tính bán kính quả bóng.
a) Diện tích bề mặt của hình cầu bán kính R là: \(V = 4\pi {R^2}\).
b) Thể tích của hình cầu bán kính R là: \(V = \frac{4}{3}\pi {R^3}\).
Bán kính quả bóng là: \(R = 24:2 = 12\left( {cm} \right)\)
a) Diện tích bề mặt quả bóng là:
\(V = 4\pi {R^2} = 4\pi {.12^2} = 576\pi \left( {c{m^2}} \right)\).
b) Thể tích của quả bóng là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.12^3} = 2304\pi \left( {c{m^3}} \right)\).

Các bài tập cùng chuyên đề
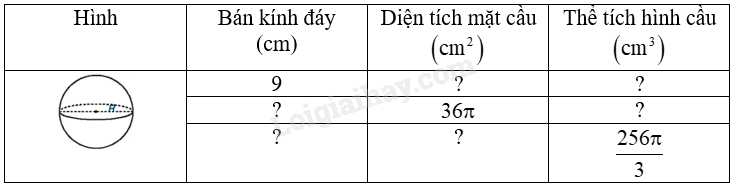
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
|
Hình |
Bán kính đáy (cm) |
Diện tích mặt cầu \(\left( {c{m^2}} \right)\) |
Thể tích hình cầu \(\left( {c{m^3}} \right)\) |
 |
3 |
? |
? |
|
? |
\(100\pi \) |
? |
|
|
? |
? |
\(972\pi \) |
Một cốc đựng ba viên kem có dạng hình cầu, mỗi viên đều có bán kính 3cm. Tính thể tích của kem đựng trong cốc (làm tròn kết quả đến hàng đơn vị của \(c{m^3}\)).
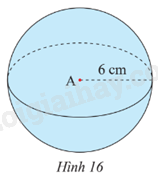
Quan sát hình cầu ở Hình 16. Hãy cho biết tâm, bán kính, diện tích mặt cầu và thể tích của hình cầu đó.
Phần bên trong của một cái li có dạng hình nón có bán kính đáy 2 cm, độ dài đường sinh 8 cm. Người ta đựng đầy kem trong li và thêm một nửa hình cầu kem phía trên (Hình 19). Tính thể tích của kem (kết quả làm tròn đến hàng đơn vị).

Một hộp bóng hình trụ chứa vừa khít 3 quả bóng tennis có đường kính 6,5 cm (Hình 5).
a) Tính diện tích bề mặt và thể tích của mỗi quả bóng.
b) Tính diện tích xung quanh và thể tích hộp bóng.

Tìm các số và đơn vị thích hợp ở ô ? để hoàn thành Bảng 9.3.

Một quả dưa hấu có dạng hình cầu với bán kính 12 cm và vỏ dày 1 cm (Hình 9.46). Tính diện tích bề mặt quả dưa hấu và thể tích vỏ dưa.

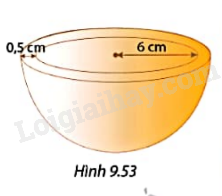
Một cái gáo nước có dạng nửa hình cầu làm từ đát sét có kích thức như Hình 9.53.
a) Hỏi gáo nước này chứa được tối đa bao nhiêu mililit nước?
b) Người ta muốn tráng men toàn bộ cái gáo nước (cả mặt trong, mặt ngoài và miệng gáo nước). Tính diện tích cần tráng men.
Cho mặt cầu có số đo diện tích bằng hai lần với số đo thể tích. Tính bán kính mặt cầu.
-
A.
3.
-
B.
6.
-
C.
\(\frac{3}{4}\).
-
D.
\(\frac{3}{2}\).
Một cái bồn chứa dầu gồm hai bán cầu và một hình trụ (như hình vẽ) (lấy \(\pi \approx 3,14\))
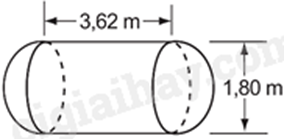
a) Bán kính của bán cầu bằng \(1,8\) m.
b) Diện tích xung quanh của bồn chứa bằng \(8,1\) \({m^2}\).
c) Thể tích của bồn chứa là \(12,26{m^3}\).
d) Lượng dầu tối đa có thể chứa được trong bồn là 3110,4 kg. biết khối lượng riêng của dầu hỏa là \(800kg/{m^3}\).
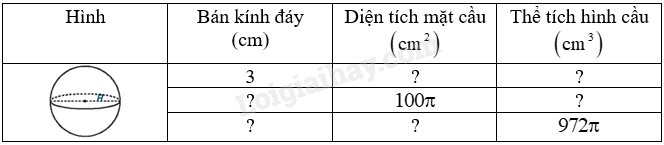
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
Cho một hình cầu có thể tích bằng \(288\pi \;c{m^3}\).
a) Tính bán kính của hình cầu.
b) Tính diện tích mặt cầu.
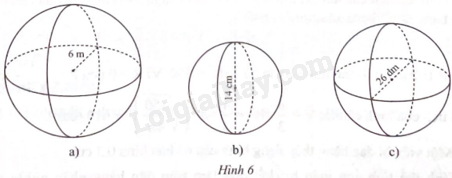
Tính diện tích mặt cầu và thể tích của mỗi hình cầu sau:
Tính thể tích của mặt cầu có diện tích mặt cầu là:
a) 170 m2
b) 190 dm2
c) 1973 cm2
(Làm tròn kết quả đến hàng đơn vị của mét vuông, đềximét vuông, xăngtimét vuông).
Cho một mặt cầu có diện tích \(576\pi \) m2 . Thể tích của hình cầu đó là
A. 2304 m3
B. \(2304\pi \) cm3
C. 2304 cm3
D. \(2304\pi \) m3
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
Quả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính 24cm. Hãy tính:
a) Diện tích bề mặt quả bóng.
b) Thể tích của quả bóng.







Danh sách bình luận