Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu?
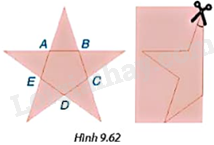
+ Tính được góc trong ngũ giác đều bằng \({108^o}\).
+ Tính được \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\) nên \(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\)
+ Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng \(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).
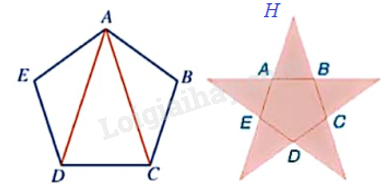
Xét ngũ giác đều ABCDE, ta thấy tổng 5 góc của ngũ giác đều đó bằng tổng các góc trong ba tam giác ABC, ACD, ADE, tức là bằng \({3.180^o} = {540^o}\). Do tất cả các góc của ngũ giác đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng \(\frac{{{{540}^o}}}{5} = {108^o}\).
Do đó, \(\widehat {EAB} = \widehat {ABC} = {108^o}\).
Suy ra: \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\).
Tam giác HAB có:
\(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\)
Do đó, góc tạo bởi lưỡi kéo và nếp gấp lúc đầu là:
\(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).

Các bài tập cùng chuyên đề
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều \({45^o}\) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
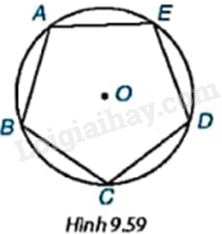
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59.
a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.
b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?
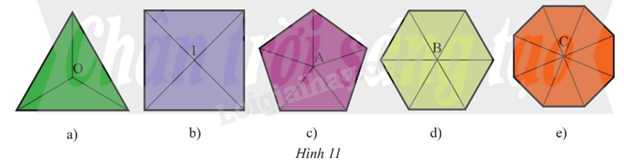
Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó.
Cho đường tròn (O; R).
a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).
b) Tính các cạnh của các hình vừa vẽ theo R.
Mái nhà trong Hình 7 được đỡ bởi khung đa giác đều. Gọi tên đa giác đó. Tìm phép quay biến đa giác đó thành chính nó.

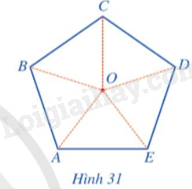
Cho ngũ giác ABCDE tâm O (Hình 31).
a) Phép quay ngược chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm nào?
b) Chỉ ra các phép quay tâm O giữ nguyên hình ngũ giác đều đã cho.
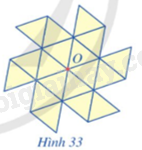
Vẽ trên giấy 18 hình tam giác đều bằng nhau và ở vị trí như Hình 33 (còn gọi là hình chong chóng).
a) Hãy đánh dấu 6 điểm mút của hình chong chóng sao cho 6 điểm mút đó là các đỉnh của một hình lục giác đều tâm O.
b) Hãy chỉ ra những phép quay tâm O giữ nguyên hình chong chóng.
Mỗi phát biểu sau đây có đúng hay không? Vì sao?
a) Đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó là đa giác lồi.
b) Tứ giác có tất cả các cạnh bằng nhau là tứ giác đều.
c) Tứ giác có tất cả các góc bằng nhau là tứ giác đều.
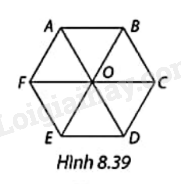
Cho lục giác đều ABCDEF như Hình 8.39.
a) Tìm ảnh của hình bình hành OABC qua phép quay thuận chiều 60o tâm O.
b) Tìm ba phép quay ngược chiều tâm O giữ nguyên lục giác đều ABCDEF.
Quan sát hình ảnh khay đựng bánh kẹo (các tam giác nhỏ trong hình là các tam giác đều bằng nhau). Các khẳng định sau đúng hay sai?
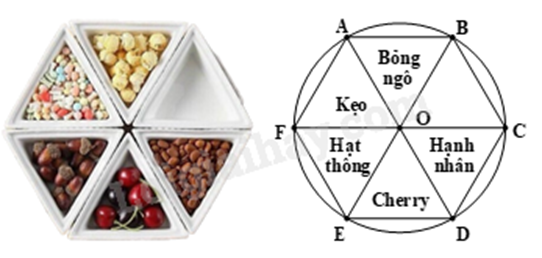
a) Khay đựng bánh kẹo này là hình lục giác đều.
b) \(\widehat {ABC} = {120^o}\)
c) Hình OABC là một đa giác đều
d) Khi giữ nguyên tâm của khay và quay một góc \({120^o}\) thì vị trí của Bỏng ngô sẽ di chuyển sang vị trí của Hạnh nhân.
Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB.
a) \(\widehat {AOB} = {50^o}\).
b) OH = OA. sin 45o
c) Phép quay 90o tâm O biến bát giác đều thành chính nó.
d) AB = 2OA . sin 22,5o.
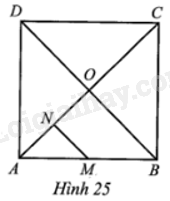
Cho hình vuông ABCD và O là giao điểm của AC và BD. Gọi M là trung điểm của AB, N là trung điểm của AO (Hình 25). Phép quay ngược chiều 90° tâm O biến các điểm N, M lần lượt thành các điểm N’, M’.
a) Chứng minh tam giác BN'M' là tam giác vuông cân.
b) Tính tỉ số diện tích tam giác ANM và diện tích tam giác CN'M'.
c) Phát biểu “Phép quay thuận chiều 90° tâm N biến điểm O thành điểm M, biến điểm D thành điểm B” là đúng hay sai? Vì sao?
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O).
a) Tính bán kính của (O) biết rằng ta lấy \(\cos {54^o} \approx 0,59\).
b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.







Danh sách bình luận