Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
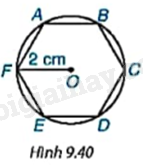
+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra
\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).
+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).
Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Do đó,
+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)
+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)
Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.
Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)
Suy ra:
\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)
Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)
Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)
Các bài tập cùng chuyên đề
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
- Vẽ đường tròn tâm O bán kính R.
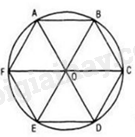
- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).
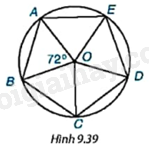
Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
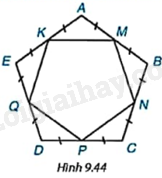
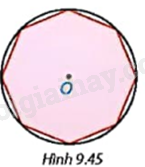
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
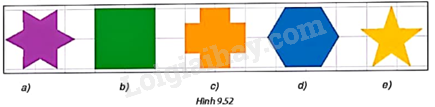
Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Cho hình thoi ABCD có \(\widehat A = {60^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
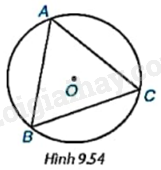
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều \({60^o}\) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung \(\overset\frown{MN},\overset\frown{NP},\overset\frown{PQ},\overset\frown{QR},\overset\frown{RM}\) bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng
A. R.
B. R\(\sqrt 3 \).
C. \(\frac{{R\sqrt 3 }}{2}\).
D. \(\frac{R}{2}\)
Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm biến tam giác ABC thành chính nó?
A. 90o.
B. 100o.
C. 110o.
D. 120o.
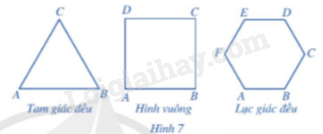
Quan sát Hình 7 và nêu đặc điểm về cạnh và góc của tam giác đều, hình vuông, lục giác đều.
Ghép sau miếng phẳng hình tam giác đều có cạnh bằng nhau để tạo thành hình lục giác ABCDEG như Hình 10. Lục giác ABCDEG có là lục giác đều hay không? Vì sao?
Cho ngũ giác ABCDE có các cạnh bằng nhau và \(\widehat A = \widehat B = \widehat C = 108^\circ .\) Ngũ giác ABCDE có phải là ngũ giác đều hay không?
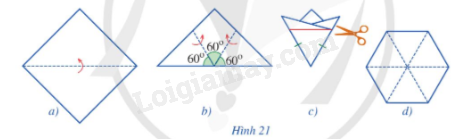
Bạn Đan gấp một tờ giấy (có dạng hình vuông) lần lượt theo Hình 21a và Hình 21b để được Hình 21c, rồi cắt theo đoạn thẳng màu đỏ như ở Hình 21c, sau đó mở ra và được tờ giấy như Hình 21d. Bạn Đan cho rằng đó là một lục giác đều, theo em, bạn Đan nói đúng hay không?
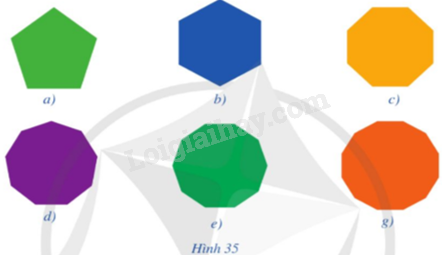
Cho các vật thể có dạng các đa giác đều như ở hình 35. Gọi tên từng đa giác đều đó.
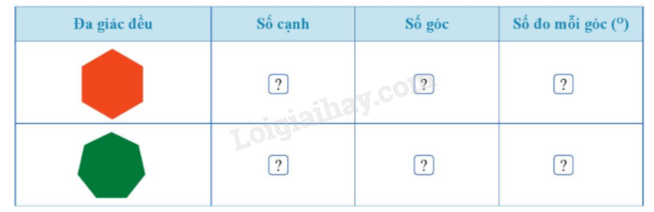
Quan sát từng đa giác đều và tìm số thích hợp vào ô trống trong bảng sau:
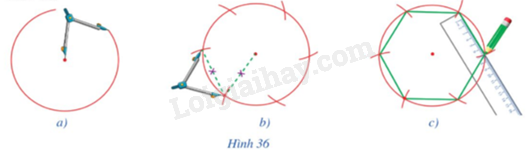
Quan sát hình 36a, 36b, 36c và dùng compa, thước thẳng để vẽ lục giác đều theo cách đó.
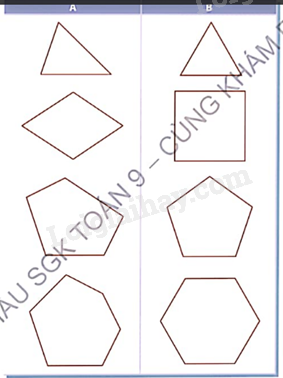
Cho các đa giác trong Bảng 8.1. So sánh các cạnh và các góc của mỗi đa giác, cho biết các đa giác ở cột B có đặc điểm gì khác so với đa giác tương ứng ở cột A.
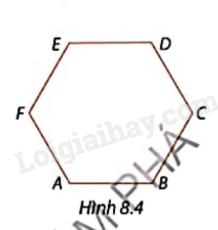
Tính số đo các góc B và E của lục giác đều trong Hình 8.4, biết \(\widehat A = {120^o}\).
Kể tên các loại đa giác đều có trong Hình 8.14.
Tìm các số thích hợp cho các ô ? trong Bảng 8.2:
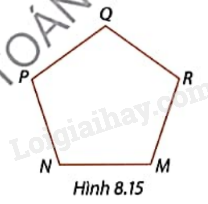
Cho ngũ giác đều MNPQR như Hình 8.15. Kể tên các đỉnh, các góc, các cạnh và đường chéo của ngũ giác đều.
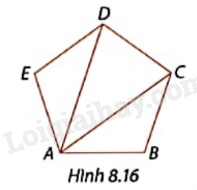
Cho ngũ giác đều ABCDE như Hình 8.16.
a) Tính tổng các góc trong tam giác ABC, ACD, ADE, từ đó suy ra tổng các góc trong ngũ giác đều ABCDE.
b) Tính số đo góc E.
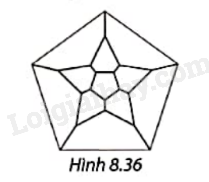
Có bao nhiêu đa giác đều trong Hình 8.36?
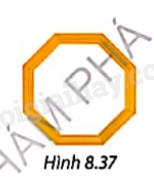
Tính số đo mỗi góc của khung gỗ trang trí có hình bát giác đều như Hình 8.37.
Chu vi của lục giác đều có độ dài cạnh 2 cm bằng
A. 8 cm
B. 10 cm
C. 12 cm
D. 16 cm
