Với điểm A cho trước nằm trên đường tròn (O), có bao nhiêu hình vuông có một đỉnh là A nội tiếp đường tròn (O)?
Với điểm A cho trước nằm trên đường tròn (O), có duy nhất một hình vuông có một đỉnh là A nội tiếp đường tròn (O).
Với điểm A cho trước nằm trên đường tròn (O), có duy nhất một hình vuông có một đỉnh là A nội tiếp đường tròn (O).
Các bài tập cùng chuyên đề
Tính cạnh của hình vuông nội tiếp \(\left( {O;R} \right)\)
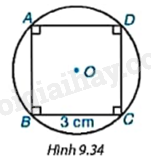
Cho hình vuông ABCD có cạnh bằng 3cm (H.9.34).
Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.
Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó.
Cho hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R.
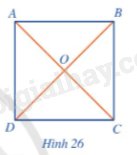
Cho hình vuông ABCD, AC cắt BD tại (O) (Hình 26).
a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?
b) Cho biết AB = a, tính OA theo a.
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó.
Xác định tâm và đường kính của đường tròn ngoại tiếp hình vuông có cạnh 3 cm.
Đường tròn ngoại tiếp hình vuông cạnh 2cm có bán kính là
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số \(\frac{R}{r}\) là:
Tính cạnh của hình vuông nội tiếp \(\left( {O;3} \right)\)
Cho hình vuông ABCD có cạnh bằng 4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính, chu vi của đường tròn đó.
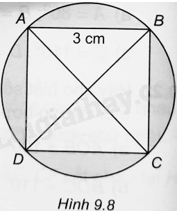
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
Cho hình thoi ABCD có cạnh bằng \(a\sqrt 2 \) và nội tiếp đường tròn (O; R). Chứng minh ABCD là hình vuông và tính bán kính R theo a.
Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) tiếp xúc với các cạnh của hình vuông. Tính theo a bán kính R và r.
Cho tứ giác ABCD nội tiếp đường tròn (O; R) và \(\widehat A = {90^o}\), BD = 12 cm. Độ dài của bán kính R là
A. 12 cm
B. 24 cm
C. 6 cm
D. \(6\sqrt 2 \)cm
Khẳng định nào sau đây là đúng?
A. Có vô số đường tròn khác nhau cùng ngoại tiếp một hình vuông.
B. Mỗi đường tròn ngoại tiếp đúng một hình vuông.
C. Hai hình vuông có cạnh bằng nhau thì cùng nội tiếp một đường tròn.
D. Hai hình vuông cùng nội tiếp một đường tròn thì có diện tích bằng nhau.
Cho hình vuông ABCD nội tiếp (O) với \(AB = 4cm\). Hãy tính diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của (O).
